Modelling of Neurons and Carcinogenesis
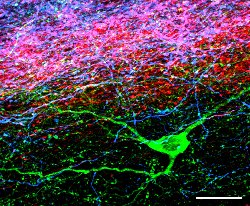 |
Confocal microscope images showing the relationship
between a neuron (green) and the locations of a particular class of
inputs. This neuron has been selectively stained and represents one
of a large population of neurons in the same area. (Picture supplied courtesy of D. Maxwell and D. Oliva, University of Glasgow) |
An understanding of the behaviour and function of the neuron - the basic building block of the central nervous system - provides a good example of the character of Mathematical Biology. A neuron (shown in green in the figure) has a complex shape and consists of a thin membrane separating an intracellular fluid, rich in potassium ions, from an extracellular fluid containing an abundance of sodium ions. It has been well known for over 100 years that neurons exhibit a vast range of geometries, and although its widely accepted that this geometry is important, its role in shaping the behaviour of a neuron is at best poorly understood. This behaviour is best understood in terms of the biophysical properties of neurons, including, for example, how ionic species inside and outside the neuronal membrane interact to generate the electrical activity characteristic of all neurons. The prevailing mathematical model for these ionic interactions is due to the Nobel Prize winning work of Hodgkin and Huxley (1953). An important task of the mathematician is reveal how the complex geometry and biophysical properties of a neuron are combined to determine its function. The analytical and numerical techniques required to achieve this objective are diverse and need to be developed through a detailed understanding of all aspects of the neuron. This is a complex task. Neuronal growth is stochastic; the inputs to and outputs from a neuron are best described as stochastic processes. Furthermore, the neuronal membrane behaves in a nonlinear fashion. Consequently the task of connecting neuronl geometry, neuron biophysical properties and function for a single neuron and a network of neurons lies firmly in the domain of the applied mathematician, physicist and electrical engineer. While neural networks have been used widely as information processing devices, its interesting to note that perhaps Nature's greatest creation, the human brain, does not resemble a neural network as it is currently understood. To understand the function of collections of neurons ( a brain), and how such a collection processes information, is one of the outstanding problems in biological mathematics of the 21st century.
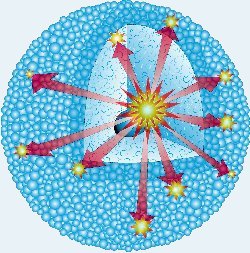 |
An advantage of the concentration in tumour cells of radionuclides with long range emissions (e.g. 131 l) is the presence of a radiological bystander effect. That is, the bombardment of untargeted cells by beta decay particles emanating from neighbouring, successfully targeted cells which have actively accumulated 131 l-labelled drug. |
The modelling of carcinogenesis is another, very different, area in which Applied Mathematics contributes to the developement of biological research and medicine. Complex biological organisms such as mammals develop through cell differentiation. This is a process in which primitive cells (stem cells) with a high reproductive capacity generate a cascade of progressively more complex cell types which become increasingly particularised to specific bodily tasks (e.g. liver cells), but in so doing lose their ability to divide. The process of cell division, however, is inherently risky and can go wrong in various ways. Normally mutations in DNA are detected by guardian genes (e.g. p53) which then prevent the cell dividing to allow derair of lesions or to set in motion cell suicide (Apoptosis). However, on the odd occasion, a damaged cell will divide successfully and in the process produce more similarly damaged cells as futher cell division occurs. As time evolves, a spectrum of cells with varying degrees of damage will develop until a malignant transformation takes place in a particular cell. This malignant cell can become the ancestor of a colony of malignant cells (a tumour). It is axiomatic that tumour cells do not recognise the body's control mechanisms and so grow uncontrollably. The number of separate mutations needed for malignant transformation is an important question as is the inheritability of these mutations. Mathematical models of carcinogenesis can answer these questions. For example, Knudson used a mathematical model to show that retinoblastoma, a cancer of the eye, requires for malignant transformation, two mutations, one of which may be inherited. These mutations occur in the Rb gene. Mathematical models of carcinogenesis also provide insight into biological mechanisms by enabling them to be simulated and comparisons drawn between the results of the simulation and observation. For example, it has been shown that a mutation in the p53 gene may not in itself constitute a stage in carcinogenesis, but could increase the likelihood that the mutations necessary for carcinogenesis will occur. Mathematical models also play a dominant role in modelling the carcinogenic risk of chemicals and radiation either as tools to control of tumours or as carcinogenic in the environment. For example, the assocation between the presence of radiation and increased risk of cancer in conjunction with the association between nuclear facilities and local increases in cancer incidence might suggest that radiation from nuclear facilities causes an increase in the local incidence of cancer. Interestingly, however, high local incidences of cancer are often experienced in remote areas devoid of nuclear facilities but with a high influx of itinerant workers. Another possible explanation for the local increase in cancer incidence is that continuous population mixing causes infections which in turn lead to increased levels of immune cell division, thereby increasing the risk of cell mutation. This important question is one that can only be answered satisfactorily by mathematics.
Some recent publications
E.G. Wheldon, K.A. Lindsay, T.E. Wheldon and J.H. Mao, A two-stage model for childhood acute lymphoblastic leukaemia: application to hereditary and non-hereditary leukaemogenesis., Mathematical Biosciences 139 , (1996) 1-24.
A.S. Hurn, K.A. Lindsay and C.A. Michie, Modelling the lifespan of human T-lymphocite subsets, Mathematical Biosciences , 143 , (1997) 91-102.
D.M. Halliday, K.A. Lindsay, J.M. Ogden and J.R. Rosenberg, Mathematical Modelling of Dendrites - Theory and Numerical Methods., (book chapter for Springer handbook on Neurophysiology).
K.A. Lindsay, J.M. Ogden and J.R. Rosenberg, Advanced numerical methods for modelling dendrites. In: Biophysical Neural Networks. ed. R.R.Poznanski .
Recent PhD students
James M Ogden (1995-1999) completed his PhD entitled "Construction of fully equivalent neuronal cables: An analysis of neuron geometry". Dr. Ogden now works in Liverpool for the Sony Corporation.
Elizabeth Wheldon (1996- ) is currently working on the impact of various agents, for example, infections and radiation, on the incidence of carcinogenesis.
