Poles, polars and duality -the algebraic version

In this section, we give an algebraic treatment of these topics.
The proofs may be obtained by clicking on the link below the statement of each theorem.

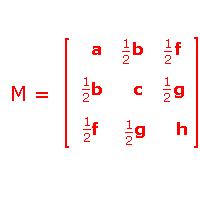
A plane conic has an equation of the form ax²+bxy +cy²+fx+gy+h=0.
In terms of homogeneous coordinates, this becomes ax²+bxy +cy²+fxz+gyz+hz²=0
which can be written as x^TMx=0 where x=(x,y,z), and M is a symmetric 3x3 matrix.

For a non-degenerate conic, M must be non-singular and have eigenvalues of different sign.

Note that, if a conic contains three (distinct) collinear points, then it must be degenerate.

Definition
If C: x^TMx=0 is a non-degenerate conic and U=[u] is any point,
then the algebraic polar of U with respect to C is the line u^TMx=0.

Note that, as M is non-singular, we cannot have u^TM=0, so that the line always exists.

A line L has an equation a^Tx=0. Now, u^TMx=0 and a^Tx=0 give the same line if and only if [u]=[M^-1a].
Thus L is the polar of a unique point U=[u].

Definition
If C: x^TMx=0 is a non-degenerate conic and L is any line,
then the algebraic pole of L with respect to C is the point U=[u] such that L has equation u^TMx=0.

Remark
If L has equation a^Tx=0, then, as we have seen, the pole of L is U=[M^-1a].

Theorem 1
If C: x^TMx=0 is a non-degenerate conic and U is any point on C,
then the algebraic polar of U with respect to C is the tangent to C at U .

Proof of Theorem 1

We now show that the algebraic polar coincides with the geometrical polar.

Theorem 2
Suppose that C: x^TMx=0 is a non-degenerate conic and that VW is a chord of C passing through a fixed point U.
Then the tangents at V and W meet on the algebraic polar of U with respect to C.

Proof of Theorem 2

It follows readily that the algebraic and geometric poles of a line coincide.

We now have the idea of duality defined in algebraic terms.
The fundamental result is that duality preserves incidence.

Theorem 3 La Hire's Theorem
Suppose that C: x^TMx=0 is a non-degenerate conic and that U and V are any points.
Then U lies on the polar of V if and only if V lies on the polar of U.

Proof of Theorem 3

From certain points in the plane, it is possible to draw tangents to the conic C.
Provided the point does not lie on the conic, there will be exactly two tangents, as the following theorem shows.

Theorem 4
Suppose that C: x^TMx=0 is a non-degenerate conic and that U is any point.
Then the pair of tangents to C from U has equation u^TMu x^TMx =u^TMx u^TMx .

Proof of Theorem 4

Together, Theorems 1, 2 and 4 establish

Joachimsthal's Formulae
Suppose that C: x^TMx=0 is a non-degenerate conic. Then

• The polar of U=[u] has equation u^TMx=0.
• If U=[u] is on C, then the tangent to C at U has equation u^TMx=0.
• The pair of tangents to C from U=[u] has equation u^TMu x^TMx =u^TMx u^TMx .

Of course, the second is really a special case of the first (but we proved it as Theorem 1 to help with the proof of Theorem 2).

We now show that the dual of a conic with respect to a fixed conic is actaully another conic.
There is a macro to draw the dual conic in the conics toolbar.

Theorem 5
Suppose that C: x^TMx=0 and D: x^TNx=0 are non-degenerate conics.
Then the dual of D with respect to C is the non-degenerate conic with equation x^TMN^-1Mx=0.

Proof of Theorem 5

Main Conics Page

Geometry Page

Main Cabri Page