Chasles Theorem
An alternative approach to Pascal's Theorem uses a beautifully simple result due to Chasles.
We begin with the dual of the cross-ratio of four points on a line, namely the cross-ratio of
four lines through a point. We refer to such a configuration as a p-pencil and the common
point as its vertex
lemma 1
If A,B,C,D are p-lines through a p-point P and L a p-line meeting
A,B,C,D in A,B,C,D respectively, then the cross-ratio (A,B,C,D)
is independent of the choice of L.
proof
This allows us to make the
definition
If A,B,C,D are p-lines through a p-point P, the cross-ratio (A,B,C,D)
is the cross-ratio of the p-points where the p-lines meet any p-line L
Since the cross-ratio of points is a projective invariant, we immediately have
lemma 2
The cross-ratio of a p-pencil is a projective invariant
If we look at an embedding of a p-pencil and p-line L, we get a pencil on the embedding
plane with vertex P and a line L cutting the lines of the pencil at A,B,C,D. The cross-ratio
of the p-pencil is equal to (A,B,C,D), and may be denoted by (PA,PB,PC,PD), though it
depends only on the lines, and not on the points chosen.
lemma 3
If a line cuts the lines of a pencil with vertex P at the points A,B,C,D,
then
(PA,PB,PC,PD) = sin(<APC)sin(<BPD)/sin(<BPC)sin(<APD).
proof
lemma 4
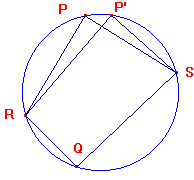
Suppose that we have five points P,P',Q,R,S on a circle.
If P,P' lie on the same side of RS, then as signed angles,
then sin(<RPS) = sin(<RP'S).
If P,Q lie on different sides of RS, then as signed angles,
then sin(<RPS) = -sin(<RQS).
proof
In the first case, the signed angles RPS,RP'S are actually equal.
In the second case, if <RPS has size θ then <RQS has size π-θ,
but if we measure them in the same sense, we get <RQS equal
to π+θ
This can be interpreted as saying that as we move P on the
circumference, the sign of sin(<RPS) changes as P passes
either R or S, but the size remains constant throughout.
|
 |
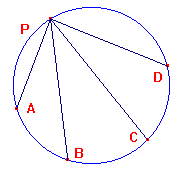
Chasles Theorem
If A,B,C,D,P lie on a conic C, then the cross-ratio (PA,PB,PC,PD)
is independent of the choice of P.
proof
Since we are dealing with a projective invariant, we can transform
the figure so that the conic becomes a circle as shown on the right.
Then the cross-ratio (PA,PB,PC,PD) can be defined in terms of the
sines of certain angles, as above.
By Lemma 4, the size of these sines do not depend on the choice
of P. As P varies, whenever it passes one of the points A,B,C,D
the signs of the two sines involving that vertex change.
It follows that the cross-ratio is constant.
|
 |
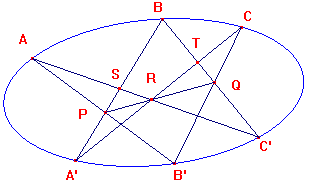
Pascal's Theorem
If A,A',B'B',C,C' lie on a conic C and AB',A'B meet in P,
BC',B'C in Q and CA',C'A in R,
then P,Q,R are collinear.
proof
By Chasles' Theorem, (AA',AB',AC',AB) = (CA',CB',CC',CB).
As remarked above, these are equal to the cross-ratios of
the points which are intersections of the pencils with BA', BC'.
Thus (A',P,S,B) = (T,Q,C',B).
Now consider these cross-ratios as those of pencils through R.
(RA',RP,RA,RB) = (RC,RQ,RC',RB). As lines, RA'=RC, RA=RC',
so the pencils have three lines in common. Since their cross-
ratios are equal, the lines RP,RQ are identical, as required.


