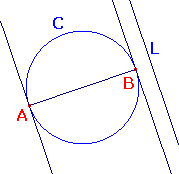
For any circle C, each family of parallel lines contains exactly two tangents
to C, and these occur at diametrically opposite points of C.
Suppose that L is a line. Let AB be the diameter of C perpendicular to L.
Let M be a line parallel to L.
- If M does not meet AB, then it does not meet the circle.
- If M cuts AB between A and B, then it cuts the circle twice -
once on each side of AB. - If M cuts AB at A or B, then it meets the circle only at this point.
To verify this, suppose that M meets C again, at P say. Then it
will meet C at a third point - the reflection of P in C. But a line
cuts a circle at most twice, so M meets C exactly once. It is the
tangent to C at this point.