Classically, a plane conic C is defined in terms of
a point F, the focus,
a line L, the directrix, and
a positive number e, the eccentricity.
Then C is the locus {P : |PF|=e|PL|},
where |PL| denotes the distance of the point P from the line L.

The CabriJava applet shows a conic with focus F, directrix L passing through a point P.
The choice of P determines the eccentricity - as the ratio |PQ|/|PF|. You can move F
and P to see what shapes are possible.
Notes.
(1) Part of the figure may be out of the picture. Indeed, when e > 1, a complete
branch may be missing.
(2) The points P' and Q' are the reflections of P and Q in the line through the focus F
perpendicular to the directrix L. This is the axis of the conic. Since |P'Q'| = |PQ| and
|P'F| = |PF|, P' also lies on the conic. Thus, each conic is symmetric in its axis. later,
we shall investigate what other symmetries a conic may have.

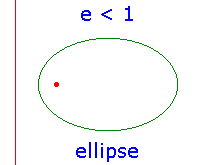
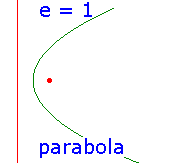
As we have seen, the shape of the conic depends on the value of e, and there are three
basic types, depending on whether e < 1, e = 1, or e > 1. These are called, respectively,
ellipses, parabolas and hyperbolas. Examples of each type are illustrated below. In each
picture, the focus and directrix are shown in red, the conic in green. Notice that the
hyperbola consists of two separate parts - the branches of the hyperbola.

Proving that the shapes are as shown is best achieved by finding an equation for a conic.
We shall get a general result for all conics, then show that, by choosing axes appropriate
to each case, we can obtain just three standard equations.

To see the effect of varying e, and what kinds of equations, we have another picture.