Since the equation of H, like that of E, involves only
square terms in x and y, the symmetry group of H is
also {e,h,v,r}.

Once again, the existence of reflection symmetries
allows us to obtain the sketch from a knowledge of
the part of the curve in the first quadrant.

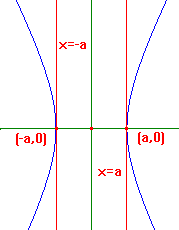
Note that H cuts the x-axis at (a,0) and (-a,0),
but does not cut the y-axis since we cannot have
a real y with - y²/b² = 1

For (x,y)εH, x²/a² = 1+ y²/b², so we have x² ≥ a²,
and hence x ≥ a or x ≤ -a. Thus, H has no points
between the lines x = -a and x = a.

Some plotting, and application of symmetry will soon
produce a picture like that on the right. The hyperbola
is shown in blue, the axes of symmetry in green. The
lines x = a and x = -a are shown in red. They are the
tangents to H at (a,0) and (-a,0).

On H, we also have y²/b² = x²/a² - 1, so that,
as x becomes numerically large, so does y. In fact,
we can quantify this in a rather nice way.

Suppose that P(x,y) is a point on H in the first quadrant.
We can factorize the right-hand side of the equation of E,
and rewrite the equation as (x/a + y/b)(x/a - y/b) = 1.
Now let x tend to ∞. As we are in the first quadrant, y>0,
so y also tends to ∞. Thus, (x/a+y/b) tends to ∞. It then
follows that the other factor (x/a-y/b) tends to 0, and,
since it positive, does so from above. This shows that
the point P will approach the line x/a-y/b = 0, and will
do so from below.

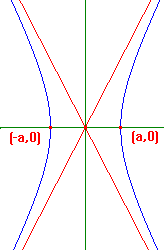
Applying reflections, we see that the hyperbola H will
approach the lines x/a - y/b = 0 and x/a + y/b = 0.
These lines are called the asymptotes of H. They are
shown in red in the lower picture.

some further notation

The point O, the centre of the rotation symmetry,
is called the centre of the hyperbola.

The x-axis is the axis of symmetry which cuts H
This is the transverse axis of the hyperbola. The
other axis of symmetry, here the y-axis, is called
conjugate axis of the hyperbola.