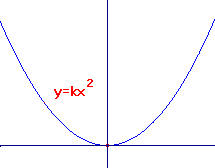
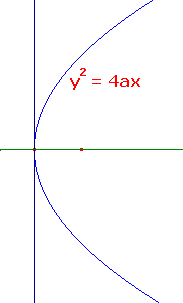We assume that the reader is amiliar with the graph of
the curve y = kx², with k > 0. This is shown in the top
sketch.

If we reflect this graph in the line y = x, then the
transformed curve will have equation x = ky². For
k = 1/4a, this is the graph of P. This is shown in the
second sketch.

We observe that the y-axis is the tangent to P at the
origin - the vertex of P.

Apart from the identity e, the only obvious symmetry
is h, reflection in the x-axis. The existence of this
symmetry is apparent from the algebra, since, if (x,y)εP,
then y = 4ax², so y = 4a(-x)², i.e. (-x,y)εP.

For the moment, we will take it as intuitive that there
are no other symmetries, so that the symmetry group
of P is {e,h}.

For P, the reflection symmetry is reflection in the x-axis.
This is the axis of the parabola.