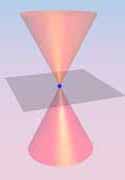
Given a point O, a line L through O, and αε(0,π/2),
the cone with vertex O, axis L and angle α consists of
all points on lines through O making angle α with L.
The lines are called the generators of the cone.
As an example, take the origin O as vertex,
the z-axis as axis,
and α = π/4. This defines
the cone K0 with equation
x2+y2=z2.
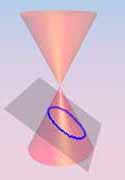
Sections of K0 by planes z = k (k ≠ 0) are circles.
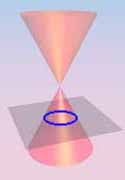
are the usual plane conics.
Note. It is far from clear that these are conics
as described
by the usual focus-directrix definition.
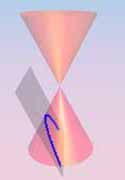
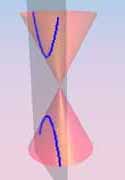
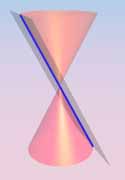
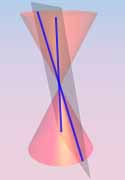
give degenerate plane conics.
Observe that each is either finite (a single point!),
or contains a line (a generator of K0).
On the other hand, it is easy to see that no
non-degenerate conic contains a line.
Theorem A plane conic is non-degenerate if