properties of trebly asymptotic triangles
(1) All trebly asymptotic triangles are hyperbolic congruent.
(2) A trebly asymptotic triangle has a hyperbolic incircle.
(3) If XYZ is a trebly asymptotic triangle and the incircle touches YZ at A,
ZX at B and XY at C, then ABC is equilateral. The excircles of ΔABC are
horocycles. Each side of ABC has length a, where sinh(½a) = ½, and each
angle is α, where cos(α)=3/5. The hyperbolic radius of the incircle is r,
where tanh(r) = ½.

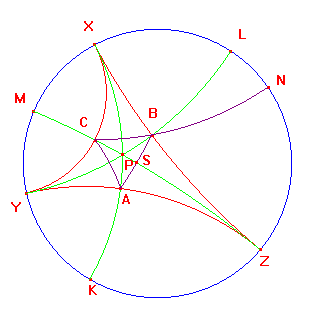
proof (1) Suppose that (X,Y,Z) and (X',Y',Z') are triples of distinct points on C. By the fundamental theorem of weird geometry, there is a unique hyperbolic transformation mapping X to X', Y to Y' and Z to Z'. Thus, the triangles XYZ, X'Y'Z' are hyperbolic congruent. (2) The axis H of the hyperbolic lines XY, XZ is the hyperbolic line XK such that inversion in H swaps XY and XZ. Clearly XK lies between XY and XZ, so crosses ΔXYZ.It therefore intersects the axis YL of YX, YZ. Let P be the intersection. By Theorem HA7, ΔXYZ has a hyperbolic incircle with centre P. This touches each side at the foot of the perpendicular from the point P. (3) We will use the notation of (2). Inversion in the hyperbolic line XK swaps XY and XZ, so swaps Y and Z. It therefore maps the hyperbolic line YZ to itself. Let A be the intersection of XK and YZ. As P, A are on XK, they are fixed by the inversion, so that AP is perpendicular to YZ, i.e. A is the foot of the perpendicular from P to the line YZ. Likewise, B, the foot of the perpendicular from P to XZ is the intersection of XZ with the axis YL of YX,YZ, and C, the foot of the perpendicular from P to XY, is the intersection of XY with ZM, the axis of XZ,YZ. It follows that, as inversion in XK swaps XY and YZ, it swaps the points B and C. Hence d(A,B) = d(A,C). Likewise, using the line YL, d(A,B) = d(B,C). Hence ΔABC is equilateral. Let the hyperbolic ray CB meet C in N, as shown. As opposite angles, <NBZ = <CBX. Since inversion in YL swaps A and C, and X and Z, <CBX = <ZBA. Thus <NBZ = <ZBA, so BZ is an external bisector at B for ΔABC. Likewise AZ is an external bisector at A. These meet at Z on C. By Theorem HA7 there is a horocycle at Z touching the sides of ΔABC, as required. Let AB, PZ meet in S. By the symmetry in ZM, <BSC = ½π. let <ZBS= θ. As <ZBS = <ZBA = <CBX, <CBX = θ. Now d(S,B) = ½a, so, by the result on the angle of parallelism, tan(θ) = 1/sinh(½a). Now <ABC = α so α + 2θ = π, and hence cos(α) = -cos(2θ). Hence cos(α) = (tan2(θ)-1)/(tan2(θ)+1) = (1-sinh2(½a))/ (1+sinh2(½a)) Using standard hyperbolic trigonometry, this becomes cos(α) = 1 - 2tanh2(½a). Also d(B,C) = a, so by the Cosine Formula for ΔSBC, cos(α) = tanh(½a)/tanh(a) = ½(1 + tanh2(½a)). Comparing these formulae for cos(α), we get tanh2(½a) = 1/5, so that cos(α) = 3/5, and then sinh2(½a) = ¼, so sinh(½a) = ½. Finally, since PB is perpendicular to XZ, the hyperbolic radius of the incircle is r = d(P,B). Now, by symmetry <BPS = π/3. Also, SP is perpendicular to AB. By the Sine Formula for ΔSPB, sin(π/3) = sinh(½a)/sinh(r), and sinh(½a) = ½, so sinh(r) = 1/3½. Then cosh(r) = 2/3½, so tanh(r) = ½.

calling page