We begin with a result which is used as the first step of an induction.

calculation 1
Suppose that A,C lie in the disk, and that x ≤ d(A,C).
Let K, K' be arcs through A and C, with K' the "larger",
The hyperbolic circle K(C,x) cuts K and K' twice, and we
can choose intersections B' on K' and B on K such that
E(A,C,B) and E(A,C,B') are positive.
Then d(A,B') > d(A,B).

Proof By our choice of x, K(C,x) cuts the hyperbolic segment CA
and hence cuts both arcs of each euclidean circle through A and C.
But the hyperbolic circle is within D, so it cuts K and K' twice.
Since it cuts two arcs defined by AC, in each case it cuts the major
once, or one of the infinite arcs once. The uniqueness of B and B' is
immediate.

Now suppose the figure is transformed so C becomes O.
Then OA is a euclidean and hyperbolic segment.
We may as well reflect K' in the line OA so P, P', the centres of
the euclidean circles defining K and K' lie on
the same side of OA. This gives the picture :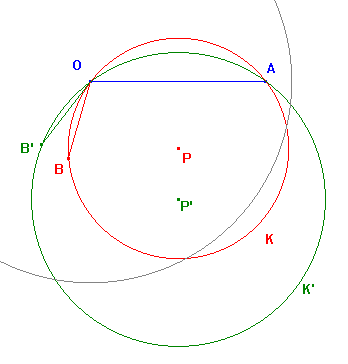

Note that OB, OB' are also euclidean and hyperbolic segments,
and < AOB, AOB' are the angles in both geometries.
Then we see that <AOB < <AOB'. The result on hyperbolic
distances now follows from the hyperbolic cosine rule.