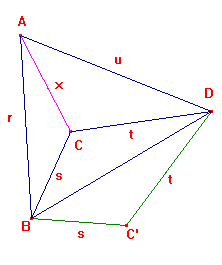
If r,s,t,u are positive numbers satisfying B(r,s,t,u) > 0, then
there is a convex quadrilateral with sides of length r,s,t,u.
proof
Suppose that r+s ≥ t+u, the x < r+s condition is unnecessary.
As indicated, we need to find x > 0 such that there are (r,s,x)
and (t,u,x) triangles. This is possible if and only if there is an x
satisfying |r-s| < x < r+s, and |t-u| < x < t+u.
The other inequalities will have solutions provided that we have
t+u > |r-s| (we know that t+u > |t-u|). The condition is thus
t+u > r-s and t+u > s-r, i.e.
s+t+u-r > 0 and r+t+u-s > 0.
As r+s ≥ t+u, r+s+t-u and r+s+u-t are positive. Hence, such x
will exist
provided B(r,s,t,u) > 0.
The case r+s < t+u is similar.
Now suppose that we have chosen such an x.
Then we can draw (r,s,x) and (t,u,x) triangles so that
the sides of length x coincide (AC), and
the vertices B,D lie on opposite sides of the line AC.
Then the sides do not intersect.
If the result is convex, we are done.
Otherwise we have a concave quadrilateral like ABCD
in the sketch. If we reflect (invert) ΔBCD in the line BD,
we get a convex quadrilateral ABC'D of the required type.
Note that , in either geometry, the angle sum for a quadrilateral
is at most 2π, so the situation like that in the picture cannot arise
at both A and C.