the circumference and area of hyperbolic circles

In euclidean geometry, the formulae for the circumference and area of a circle
can be obtained by considering the perimeter and area of a regular polygon
E(n) of n sides drawn within the circle. As n increases, the polygon expands
to fill the circle. Thus the limits as n -> ∞ give the circumference and area.

We use the same idea in hyperbolic geometry, though we replace E(n) by a
hyperbolic polygon H(n) symmetric about C, the hyperbolic centre of the circle.
If A and B are consecutive vertices of P(n), then <ACB is 2π/n.

hyperbolic circle formulae
A hyperbolic circle with hyperbolic radius r has
hyperbolic length C(r) = 2πsinh(r),
hyperbolic area D(r) = 4πsinh2(r/2).

proof
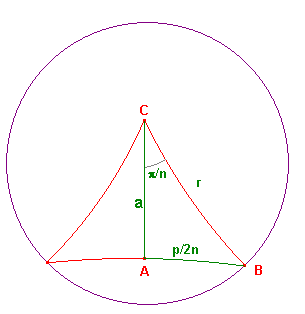
Suppose that the hyperbolic polygon H(n) introduced above has
hyperbolic perimeter p and hyperbolic area d. The hyperbolic
segments from the centre C to the vertices divide H(n) into n equal
hyperbolic triangles. The figure on the right shows one traingle in
red. the green segment is the perpendicular from C to the side of
the polygon. By symmetry it bisects the side and the angle at C.
Thus the hyperbolic triangle CAB has d(A,B) = p/2n, <ACB = π/n.
Also d(C,A) = r, the hyperbolic radius. Let d(C,B) = a, as shown.
Finally, since there are 2n such triangles, each has area d/2n.

From the sine formula for ΔABC, sin(π/n) = sinh(p/2n)/sinh(r).
Thus nsin(π/n)sinh(r) = nsinh(p/2n). Now let n -> ∞. Clearly p -> C(r).
By the limit lemma for sin and sinh, we get πsinh(r) = C(r)/2,
which gives the required result for C(r).

Since ΔABC is right-angled, the area formula gives
sin(d/2n) = sinh(a)sinh(p/2n)/(cosh(r)+1), so that
2nsin(d/2n) = sinh(a)2nsinh(p/2n)/(cosh(r)+1).
Now let n -> ∞. Then d -> D(r), a -> r and p -> C(r).
By the limit lemma for sin and sinh, we get
D(r) = sinh(r)C(r)/(cosh(r)+1) =2πsinh(r)sinh(r)/(cosh(r)+1).
Now sinh(r) = 2sinh(r/2)cosh(r/2), and cosh(r)+1 = 2cosh2(r/2),
so we get D(r) = 4πsinh2(r/2).

hyperbolic area