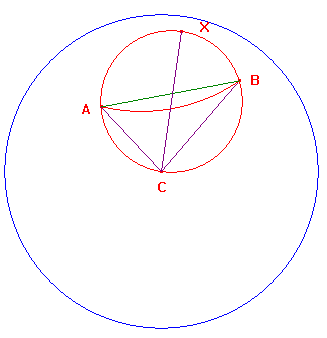
By the origin lemma, we can map C to the centre of the disk.
We will suppose that this has been done. Then CA and CB are
segments in both the euclidean and hyperbolic sense. Also the
angle ACB is the same in the euclidean and hyperbolic triangles
defined by A, B and C. Let it be denoted by θ.
Let K denote the euclidean circle through A, B and C.
This has euclidean radius R, where 2Rsin(θ) = |AB|.
This circle will lie entirely within the disk if and only if
its diameter has length less than 1.
Thus K is a hyperbolic circumcircle if and only if
|AB| < sin(θ).
By the distances theorem, |AB| = s(AB)/c(CA)c(CB).
By the sine rule, sin(θ) = Δ/sinh(d(C,B))sinh(d(C,A))
= Δ/4s(CA)c(CA)s(CB)c(CB).
Thus the condition is equivalent to that in the statement.
Now suppose that the condition holds.
Let CX be the euclidean diameter of K.
Then CX is an axis of symmetry of K.
But CX is also a hyperbolic segment.
By the symmetry, CX is a hyperbolic diameter.
Thus the hyperbolic radius is r, where d(C,X) = 2r.
Since C is the centre of the disk, d(C,X) = 2arctan(|CX|),
so that tanh(r) = |CX| =2R (the euclidean diameter).
In the above calculations, we saw that 2R = |AB|/sin(θ),
and that |AB|/sin(θ) = 4s(AB)s(BC)s(CA)/Δ.
The result follows.