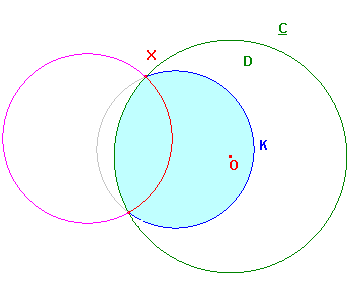
If a circle K meets the boundary C at X and Y, then
(a) K divides D into two regions, S and T,
(b) the hyperbolic line XY lies entirely in one, S, say,
(c) S is convex.
(a) is simple - the circles K and C meet only at X,Y.
(b) Let H be the i-line defining the hyperbolic line XY.
H and K meet in X,Y, and hence, as i-lines, nowhere else.
Thus the line XY lies on one side of K. We call the region
of D containing XY the region S.
(c) Let A,B be points in S. By applying the origin lemma
we may assume that A is the origin.
There are two cases, depending on whether the blue arc XY
lies on the same side of the red arc XY as O, or on the
opposite side. These are shown on the right.
Note that, in either case, since the red arc is a hyperbolic
line, it is orthogonal to C. it follows that the (euclidean)
radii OX,OY are tangents to the red circle.
In the top picture, any line through O leaves K twice.
Either twice through the blue arc, or once through the blue
arc and then crosses the red arc, leaving C through
the green arc XY, meeting K again outside C.
In either case, any segment OB lies within S.
In the lower picture, any line through O leaves C twice.
Either twice through the green arc XY on the opposite
side from the blue arc XY, or once through this green
arc and crosses the red arc, leaving S through the blue
arc XY. It meets K again outside C.
In either case, any segment OB lies within S.