If A, B, C and D are points of D0 with no three on an h-line, then
the h-quadrilateral ABCD consists of the h-segments AB, BC, CD
and DA.
The CabriJava window on the right allows you to experiment.
By dragging the vertices, you should be able to see that there
are essentially three types of h-quadrilateral. In the figure,
we have added the h-segments AC and BD. These are the
diagonals
of ABCD. Observe that these may or may not meet.
The three types are illustrated below.
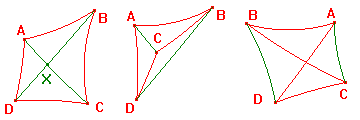
that the h-segments AC and BD (the diagonals) intersect.
Note that hyperbolic transformations preserve incidence, so
that convex h-quadrilaterals map to convex h-quadrilaterals.
For a convex h-quadrilateral, either diagonal divides the
figure into two h-triangles. Since the sum of angles of an
h-triangle is less than π, we have
The h-quadrilateral Theorem
The sum of internal angles of a convex h-quadrilateral is
less than 2π.