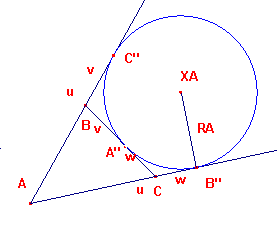
three excircles. Each centre is determined by angle bisectors (either all internal, or
two external). If it exists, the excircle arising from the external bisectors at B and C
is the excircle opposite A. Its radius is denoted by RA. The radius of the incircle is R.
The cabrijava applet allows you to experiment in the hyperbolic plane.
We begin with some results in neutral geometry.
lemma
(1) Suppose that the incircle of ΔABC meets the sides as shown, and that
AC'=x, BC'=y, CA'=z. Then x=s-a, y=s-b, z=s-c.
(2) Suppose that the excircle opposite A of ΔABC exists, and meets the
sides as shown, and that AC"=u, BC"=v, CA"=w. Then u=s, v=s-c, w=s-b.
proof
Both parts rely on the fact that, if P lies outside a circle C, then the tangents
from P
to C are of equal length since the figure is symmetric in the line
through P and the centre of C.
For (1) we then have x+y=c, y+z=a, z+x =b. Adding these x+y+z=s, and
the
results follow.
(2) is similar.
We now specialize to hyperbolic geometry, though there are euclidean analogues.
inradius theorem
The inradius R of the hyperbolic ΔABC satisfies
(1) tanh(R) = sinh(s-a)tan(½α) = sinh(s-b)tan(½β) = sinh(s-c)tan(½γ), and
(2) tanh(R) = Δ/2sinh(s),
(3) tanh(R) = Φ/4cos(½α)cos(½β)cos(½γ).
exradius theorem
If the hyperbolic ΔABC has an excircle beyond A, then its radius RA is given by
tanh(RA) = sinh(s)tan(½α)= Φ/4cos(½α)sin(½β)sin(½γ).
This is easy - the first follows from the fact that d(A,B") = s, by the lemma, and
an application of the Tangent Formula to ΔAB"(XA). The second follows from
the first by the s-theorem.
Notes
(1)A simple consequence is that a hyperbolic triangle has two excircles of equal
radius if and only if it is isosceles, and hence three if and only if it is equilateral.
(2)It also gives a necessary condition for the existence of the excircle, namely
that sinh(s)tan(½α) < 1.
We wish to establish a necessary and sufficient condition for the existence of
excircles. This requires an existence theorem for hyperbolic triangles.
the existence theorem for excircles
Suppose that the hyperbolic triangle ABC has <CAB = α, <ABC = β, <BCA = γ. Then
there is an hyperbolic excircle opposite C if and only if cos(½γ) < sin(½α)+sin(½β),
and a horocyclic excircle opposite C if and only if cos(½γ) = sin(½α)+sin(½β).