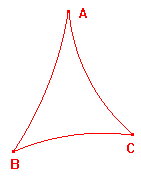
Suppose that ABC is an h-triangle.
(1) If d(A,B) = d(A,C) then <ABC = <ACB.
(2) If <ABC = <ACB then d(A,B) = d(A,C).
Consider the h-triangles ABC and ACB.
The order of vertices is significant, so we use different colours!
(1) We have
d(A,B) = d(A,C),
d(A,C) = d(A,B),
d(A,B) = d(A,C),
Thus, the h-triangles are h-congruent by the (SSS) condition.
It follows that <ABC = <ACB.
(2)
Is similar, using the (ASA) condition; we leave it as an exercise.