If L is an h-line not through any vertex of an h-triangle ABC such that
L meets AB in P, BC in Q, and CA in R,
then h(A,P,B)h(B,Q,C)h(C,R,A) = -1.
A little consideration shows that, if we change the labels of the vertices,
then either the factors are simply permuted, or are inverted and permuted.
Since our aim is to show that the product is -1, the labelling of the vertices
of the h-triangle is immaterial.
It follows that there are two cases, depending on the position of the h-line
L = PQR relative to the H-triangle.
Observe that either one cut is external, or all three are external.
It follows that the product of the ratios is negative. It is therefore
enough to show that the absolute value is +1.
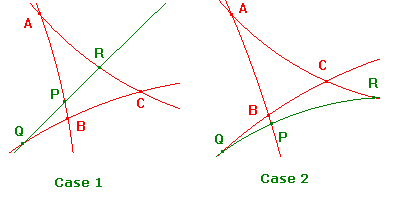
Case 1
Applying the Hyperbolic Sine Rule to the h-triangle APR,
sinh(d(A,R))/sin(<APR)) = sinh(d(A,P))/sin(<ARP).
Similarly, from the h-triangles BPQ and CRQ,
sinh(d(B,Q))/sin(<BPQ)) = sinh(d(B,P))/sin(<BQP), and
sinh(d(C,R))/sin(<CQR)) = sinh(d(C,Q))/sin(<CRQ).
Observe that:
<APR = <BPQ, so sin(<APR) = sin(<BPQ),
<BQP = <CQR, so sin(<BQP) = sin(<CQR), and
<ARP = π - <CRQ, so sin(<ARP) = sin(<CRQ).
Some elementary algebra now yields
|h(A,P,B)h(B,Q,C)h(C,R,A)| = 1.
Case 2
This follows in a similar way, with minor changes in the argument
showing that the sines of the relevant angles are equal.
Note. Essentially the same argument works in the euclidean case.