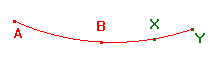
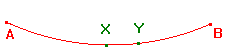If Xand Y are points on the h-line AB such that h(A,X,B) = h(A,Y,B),
then X = Y.
There are three cases, depending on whether the common hyperbolic
ratio is in (0,1), (-∞,-1) or (-1,0).
Ratio in (0,1)
Then X and Y lie between A and B. Interchanging the labels X and Y
if necessary, we may assume that Y is between X and B, as shown.
By property D3, we have, if X ≠ Y,
d(A,Y) = d(A,X) + d(X,Y) > d(A,X), and
d(Y,B) = d(X,B) - d(X,Y) < d(X,B).
Since sinh is increasing, this gives h(A,Y,B) > h(A,X,B).
Thus, if h(A,X,B) = h(A,Y,B), then X = Y.
Ratio in (-∞,-1)
Then X and Y lie beyond B. Interchanging the labels X and Y
if necessary, we may assume that Y lies beyond X, as shown.
By property D3, we have, if X ≠ Y,
d(A,Y) = d(A,X) + d(X,Y) = α + δ, say, and
d(B,Y) = d(B,X) + d(X,Y) = β + δ, say.
Thus, if h(A,X,B) = h(A,Y,B), then,
-sinh(d(A,X)))/sinh(d(X,B)) = -sinh(d(A,Y))/sinh(d(Y,B)).
So that
0 = sinh(α+δ)sinh(β)-sinh(β+δ)sinh(α)
= sinh(δ)sinh(β-α).
Thus δ = 0, or α = β, either of which implies that X = Y.
Ratio in (-1,0)
This follows from the previous case as h(A,Z,B) = 1/h(B,Z,A) for all Z.