Suppose that A, B and Q lie on a hyperbolic line H with d(A,B) = t > 0.
Then
(1) e-t < cosh(d(A,Q))/cosh(d(B,Q) < et, and
(2) for s ε (e-t,et), there is a unique Q on H with cosh(d(A,Q))/cosh(d(B,Q)) = s.
Let a = d(A,Q), b = d(B,Q). Observe that, for x ≥ 0, 0 ≤ tanh(x) < 1.
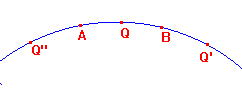
(1) There are really three case,
(a) Q beyond B (e.g. Q' in figure).
Here a = b+t, so, by the Addition Formula for cosh,
cosh(a)/cosh(b) = cosh(t)+tanh(b)sinh(t)
Using the inequalities for tanh(b),
cosh(t) ≤ cosh(a)/cosh(b) < cosh(t)+sinh(t) = et.
(b) Q between A and B (e.g. Q in figure).
Here a = t-b, with b ≤ a, so we get
cosh(a)/cosh(b) = cosh(t)-tanh(b)sinh(t).
Using the inequalities 0 ≤ tanh(b) ≤ tanh(t),
cosh(t)-tanh(t)sinh(t) < cosh(a)/cosh(b) ≤ cosh(t).
Note that, from the hypertrigonometric identities,
cosh(t)-tanh(t)sinh(t)=1/cosh(t).
Thus, in this case 1/cosh(t) ≤ cosh(a)/cosh(b) ≤ cosh(t).
(c) Q beyond A (e.g. Q" in figure).
If we reverse the roles of A and B and use the argument of (a),
cosh(t) ≤ cosh(b)/cosh(a) <et.
Inverting,
e-t ≤ cosh(a)/cosh(b) < 1/cosh(t).
Combining these, we get (1).
(2) The proof of (1) shows that the position of such a Q relative to A, B
is determined by whichever of the disjoint intervals
(e-t,1/cosh(t)),
[1/cosh(t),cosh(t)], (cosh(t),et) contains s.
In a given subinterval, the proofs of (a), (b), (c) show that the value
of s determines tanh(b) uniuely. Since tanh is bijective on [0,∞), this
determines b. Since we know which side of B contains Q, this distance
determines Q.