A saccheri quadrilateral is determined by the lenghts of its base and sides. It follows that these values determine the summit angles and area as well as the length of the summit. the summit angle and area theorem Suppose that the hyperbolic saccheri quadrilateral S has base of length c, summit of length a and sides of length d. Then the summit angle α and the hyperbolic area S are determined by the formulae : (1) cos(α) = sinh(d)sinh(½c)/cosh(½a) (2) sin(α) = cosh(½c)/cosh(½a), (3) tan(½S) = sinh(d)tanh(½c) proof Note The first part shows that cos(α) is positive. Since αε(0,π), this means that α is acute. Saccheri showed that, in any geometry, α could not exceed a right angle. As we have indicated, α = ½π occurs in euclidean geometry. We now know that, in hyperbolic geometry, α < ½π. Thus, examination of summit angles determines whether we are working in a euclidean plane or a hyperbolic plane. 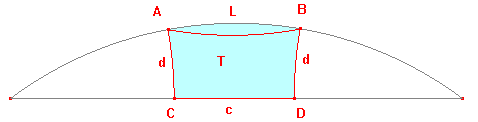A saccheri quadrilateral ABDC with base CD has A,B on a hypercircle associated with the hyperbolic line CD. It has width d, where d is the side of the quadrilateral. The segments AC,CD,CD and the hypercircle define a finite region T. an area theorem If ABCD is a saccheri quadrilateral with base CD of length c, and sides of length d, then the region T defined above has area T = sinh(d)c. proof If we split the base CD into n equal segments, then each has length c/n. By part (3) above, the total area of the saccheri quadrilaterals on each segment is S, where tan(S/2n) = sinh(d)anh(c/2n), so 2ntan(S/2n) = sinh(d).2ntanh(c/2n). As n tends to ∞, S tends to T, so 2ntanh(S/2n) tends to S. Also, 2n tanh(c/2n) tends to c. This gives the result. Note that, by an earlier result, the length of the finite arc AB is L = cosh(d)c. We thus have the strange result that, as d tends to ∞, T/L tends to 1.

previous page