the summit angle and area theorem Suppose that the hyperbolic saccheri quadrilateral S has base of length c, summit of length a and sides of length d. Then the summit angle α and the hyperbolic area S are determined by the formulae : (1) cos(α) = sinh(d)sinh(½c)/cosh(½a) (2) sin(α) = cosh(½c)/cosh(½a), (3) tan(½S) = sinh(d)tanh(½c)
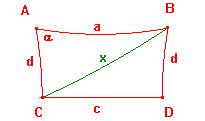
proof The sketch shows the quadrilateral labelled so that the base is CD and the summit is AB. The summit angle is α. We have drawn the diagonal BC of hyperbolic length x.
(a) cosh(x) = cosh(d)cosh(c). (b) sinh(½a) = cosh(d)sinh(½c). (c) cosh(t) = 2sinh2(½t)+1, (d) cosh2(t)-sinh2(t) = 1, (e) sinh(t) = 2 sinh(½t)cosh(½t).	Pythagoras, ΔBCD. saccheri theorem hyperbolic identities
From ΔABC, cos(α) = (cosh(a)cosh(d)-cosh(x))/sinh(a)sinh(d) Using (a), cos(α) = cosh(d)(cosh(a)-cosh(c))/sinh(a)sinh(d) Using (c) for cosh(a) and cosh(c), we get cos(α) = cosh(d)(sinh2(½a))-sinh2(½c))/sinh(a)sinh(d) Using (b) and (d), we get cos(α) = cosh(d)sinh(d)sinh2(½a)/sinh(a) Using (b) and (e), we get cos(α) = sinh(d)sinh(½c)/cosh(½a)	cosine rule
We use the standard result sin2(α) = 1-cos2(α). sin2(α) = 1 - sinh2(d)sinh2(½c)/cosh2(½a) = (cosh2(½a) - sinh2(d)sinh2(½c))/cosh2(½a) = (1+sinh2(½a) - sinh2(d)sinh2(½c))/cosh2(½a) = (1+ cosh2(d)sinh2(½c) - sinh2(d)sinh2(½c))/cosh2(½a) = (1+sinh2(½c))/cosh2(½a) = (cosh2(½c))/cosh2(½a) Now cos(α) > 0, so α is acute, and so sin(α) > 0. Thus, sin(α) = cosh(½c)/cosh(½a).
For the last part, the extension of the gauss-bonnet formula to quadrilaterals shows that S = 2π - (sum of angles of ABDC), so S = π-2α, and hence ½S = ½π-α. It follows that tan(½S) = cot(α). Thus (3) follows from (1) and (2). This determines S since ½S is in (0,½π).

previous page