Suppose that ABC and PQR are h-triangles.
Then there is a hyperbolic transformation t which maps
A to P,
B to B' on the h-line PQ, on the same side of P as Q, and
C to C' on the same side of the h-line as R.
Note that, as t preserves angle and hyperbolic distance,
d(A,B) = d(P,B'), d(A,C) = d(P,C'), d(B,C) = d(B',C'), and
<ABC = <PB'C', <BAC = <B'PC', <ACB = <PC'B'.
If h-triangles ABC and PQR have
| (1) d(A,B) = d(P,Q), |
| (2) d(A,C) = d(P,R), and |
| (3) d(B,C) = d(Q,R), |
Let t be the transformation implied by the Basic Strategy.
Then B' lies on the h-line PQ.
By the Basic Strategy, d(A,B) = d(P,B').
By (1), d(A,B) = d(P,Q), so d(P,B') = d(P,Q), and hence B' = Q.
By the Basic Strategy and (2), (3)
(4) d(P,C') = d(P,R), and
(5) d(B',C')= d(Q,C')(as B' = Q) = d(Q,R).
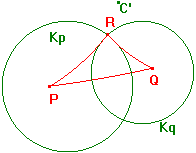
Let Kp be the h-circle, with h-centre P, through R, and
let Kq be the h-circle, with h-centre Q, through R.
By (4) and (5), C' lies on Kp and Kq
By the Basic Strategy, C' and R lie on the same side PQ.
Since Kp and Kq are h-symmetric about PQ, the h-circles
meet only once on each side of PQ, so we must have C' = R.
Thus t maps ABC to PQR, i.e. the h-triangles are h-congruent.