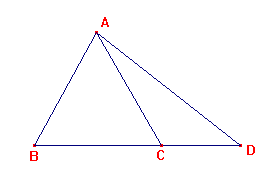
In triangle ABC, if D lies on the line BC and the segments have lengths
|AB|=c, |BC|=a, |CA|=b, |AD|=d, |BD|=m, |DC|=n, then
(1) if D lies between B and C, then a(d2+mn) = mb2+nc2,
(2) if D lies beyond C, then a(d2-mn) = mb2-nc2,
(3) if D lies beyond B, then a(d2-mn) =-mb2+nc2.
By the Cosine Rule applied to triangles ABD, ADC, we have
cos(<ADB) = (d2+m2-c2)/2dm, cos(<ADC) = (d2+n2-b2)/2dn.
(1) Here <ADC = π-<ADB, so cos(<ADC)=-cos(<ADB), so that
(d2+n2-b2)/2dn = -(d2+m2-c2)/2dm.
Simplifying this, we get
(m+n)(d2+mn) = mb2+nc2. As m+n=a, we have (1).
(2) Now <ADC = <ADB, so we get
(d2+n2-b2)/2dn = (d2+m2-c2)/2dm.
Simplifying this, we get
(m+n)(d2-mn) = mb2-nc2. As m-n=a, we have (2).
(3) The algebra is identical
to that in (2), but here n-m=a, so
we get (3).
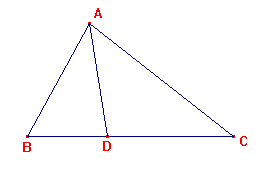
case (2)