Suppose that we have three distinct i-lines.
We can choose a point C, other than ∞, which does not lie on any of the i-lines.
If we invert the diagram in a circle with centre C, then, as the i-lines do not pass through C, they map to circles.
Thus it is enough to consider just the situations involving three circles.
In practice, it is best to use this simplification to split the problem into several cases, depending on how the
circles intersect (if at all). In each case we can apply a well-chosen inversion to simplify the analysis.
At several points of the discussion, we need to observe the following, fairly obvious:
Basic Theorem
(1) If a line L touches a circle M at a point P, then all points of L apart from P lie outside M.
(2) If circles L and M touch at P, then the points of L apart from P are all outside or all inside M.
Both follow immediately from the observation that, if the objects touch at P, then they meet nowhere else.
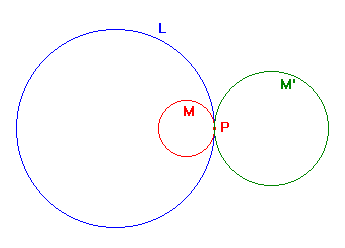
The image below shows examples of part (2). We say that L, M touch internally, and L, M' externally.
Note that, in the case of internal contact, one lies inside the other. Thus, we really have two cases.
We have shown the one where M lies inside L.

The cases: