Apollonius Theorem Ak(A,B) is a line if k is 1, and a circle if k is not 1. A and B are inverse with respect to Ak(A,B). If A and B are inverse with respect to an i-line L, then L = Ak(A,B) for some k.

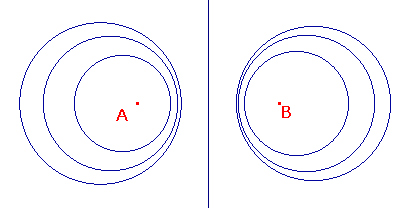
Proof We choose the perpendicular bisector of AB as the y-axis, and the line AB as the x-axis, so if A is (a,0), then B is (-a,0). Then P(x,y) lies on Ak(A,B) if and only if PA = k.PB. Squaring, we get (x-a)2 + y2 = k2{(x+a)2 + y2 }. Rearranging, we have (k2-1)(x2 + y2 + a2) + 2a(k2 +1)x = 0. If k = 1, this gives the line x = 0 (the perpendicular bisector of AB). Otherwise, we can divide by (k2 -1) to get the circle x2 + y2 + 2ax(k2+1)/(k2-1) + a2 = 0. To prove the other two parts, we begin by considering when A and B are inverse with respect to a circle C, centre F, radius r. Since B is inverse to A, B must lie on FA, so F is on AB, the x-axis. Thus,F is of the form (f,0). Note that, A and B must lie on the same side of F, so |f| > |a|. Finaly, we require that FA.FB=r2, i.e. |f-a||f+a| = r2. As |f| > |a|, this becomes f2 - a2 = r2. Thus, A and B are inverse with respect to C if and only if C has equation (x-f)2 + y2 = r2. Multiplying out, and using f2 - a2 = r2, we get x2 + y2 -2fx + a2 =0. Part two follows at once, since Ak(A,B) has this form (k not 1). Obviously, the only line with A and B inverse is the perpendicular bisector. For the third part, we need to show that any circle x2 + y2 -2fx + a2 =0 belongs to A(A,B). Given the form of the general member of A(A,B) established in part one, we need only check that we can choose k with a(k2+1)/(k2-1)=-f. A little manipulation shows that this requires k2=(f+a)/(f-a) = (f+a)2/(f2-a2). Since we must have f2 > a2 for C a real locus, we see that The value for k2 is positive, so k exists.

apollonian families