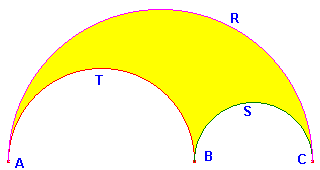
The Arbelos If three semicircles R, S and T touch at A, B and C, Then there exists an infinite family of circles {C1,C2,...} such that C1 touches R, S and T, for n > 1, Cn touches R, S and Cn-1 This result is called the arbelos since the shape bounded by the semicircles resembles that of an arbelos - a knife used by Greek shoemakers.
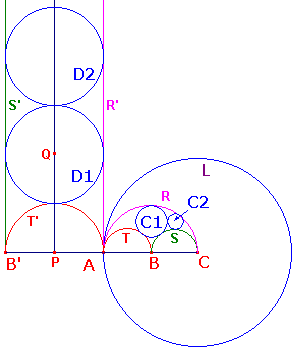
Proof As usual, we invert the picture in a well-chosen circle. Let L be the circle centre C, passing through A. As A is on L, it is fixed by the inversion. As C is the centre, it maps to Ñ. Suppose that B maps to B' (on the ray CA, of course). It follows that R and S map to parts of extended lines, R', S', perpendicular to CB', as shown. As T is not through C, it maps to T', the semicircle on diameter AB'. Now it is clear that we can draw D1 touching R', S' and T'. It must have the same diameter as T' since it touches R' and S'Its centre must be Q, vertically above P, the mid-point of AB'. Finally QP =AB' since it touches T'. It is easy to see that we can add a further circle, D2, touching R', S' and D1. Thus we can obtain a chain {Dn}. When we invert these in L, we get the required Cn.
The CabriJava plane allows you to experiment. The first five circles of the chain are shown. Drag A, B or C to change the picture. A web page just for the arbelos

Main inversive page