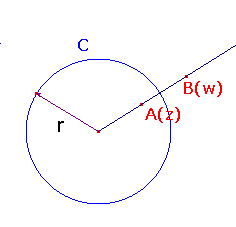
Take z non-zero, and let A be the point with complex coordinates z,
and suppose that A has inverse B (coordinates w) with respect to C.
By the definition of inverse points,
B lies on the ray OA, so w = kz, with k > 0,
and OA.OB = r2, i.e. |z|.|w| = r2.
Hence k|z|2 = r2, so k = r2/|z|2
Then w = kz = k.r2/(z.z*) = r2/z*.
The result for 0 and Ñ is obvious.