Proof of the Inversion Theorem

The Inversion Theorem

Let C be a circle with centre O.
For any object X, let X' denote the inverse of X with respect to C.

  1. If L is an extended line through O, then L' = L
  2. If L is an extended line not through O, then L' is a circle through O.
  3. If D is a circle through O, then D' is an extended line through O
  4. If D is a circle not through O, then D' is a circle not through O
Proof

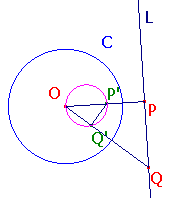
1. Suppose that P is a point on L (other that Ñ or O).
Then, by clause (1) of the definition of inversion, P' lies on L.
Since inversion in C interchanges O and Ñ, the result follows.

2. Let P be the foot of the perpendicular from O to L.
Suppose that Q is a point on L (other that Ñ or P), so <QPO is right.
By the Equal Angles Theorem, <QPO = <OQ'P', so <OQ'P' is a right angle.
Then Q' lies on the semicircle on OP' as diameter. since Ñ maps to O, we are done.

3. As inversion has order 2, (3) is equivalent to (2).

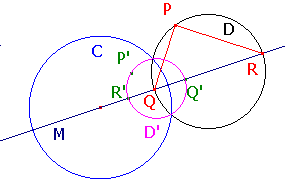
4. Let M denote the line joining O to the centre of D.
Suppose this cuts D at Q and R, so that QR is a diameter of D.
Now let P be a point on D, other than Q or R.
As an angle in a semicircle <QPR is a rigth angle.
As Q and R are on D, Q' and R' will lie on D'.
By the Corollary to the Equal Angles Theorem,
<:QPR = <R'P'Q', so the latter is also a right angle.
Thus, P' lies on the circle on Q'R' as diameter.
It follows that D' is precisely this circle.

The Inversion Theorem