Steiner's Porism

Suppose that a circle C lies inside circle D, and that circle E touches both of them. We can draw a sequence of circles, each touching C and D and the previous member of the sequence. There are two possibilities, either the sequence finishes, with the last circle touching E (upper picture), or the last circle cuts E (lower picture). In the first case, we call the sequence a Steiner Chain. Steiner's Porism If we have a Steiner Chain for one choice of E, then any other choice of E results in a Steiner Chain with the same number of circles. The proof is quite simple. Note that C and D are non-intersecting i-lines. 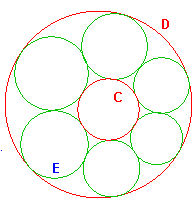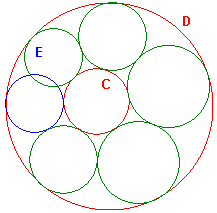By the Concentric Circles Theorem, we can invert the figure so that the images of C and D are concentric. The starting circle will invert into an i-line touching both, i.e. to a circle.

Since the figure is symmetric about the common centre P, it is clear that, if starting with E gives a Steiner Chain, then starting with F will give the Steiner Chain obtained by rotation. Clearly, it will contain the same number of circles. The CabriJava pane on the right shows a typical Steiner Chain (the red circles are non-concentric). If you move your mouse over the pane, you should see the chain rotating about the inner circle.

Main inversive page