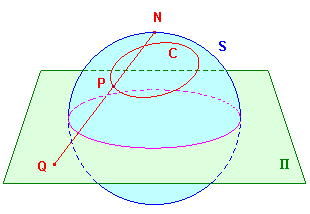
Let p denote stereographic projection with vertex N
from
the sphere S to the plane P.
Then, for any circle C on S,
p(C) is
a line if N lies on C, and
a circle otherwise.
We choose coordinates so that S is the sphere x²+y²+z² = 1
and N is the point (0,0,1) We take as P the plane z=0.
Suppose that P on S has projection Q on P.
Then Q = (X,Y,0) for some X and Y and P is the point
where NQ cuts S.
Suppose that C lies on the plane F: ax+by+cz = d.
A point on NQ has the form (tX,tY,1-t) for some real t.
This is on S if and only if (tX)²+(tY)²+(1-t)² = 1.
Simplifying, we get t((X²+Y²+1)t-2)=0.
Now, t=0 gives N, so P must have t=2/(X²+Y²+1).
But P also lies on F, so that
2aX/(X²+Y²+1) +2bY/(X²+Y²+1) + c(1-2/(X²+Y²+1) = d.
Simplifying, 2aX + 2bY - 2c = (d-c)(X²+Y²+1).
Thus the points on C project to points on the curve
2ax + 2by - 2c = (d-c)(x²+y²+1).
If c=d, this is a line, otherwise it is a circle.
Finally, we note that c=d if and only if N = (0,0,1) lies on F.