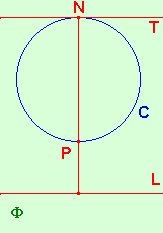
Throughout this page, we will consider stereographic projection p with vertex N from the sphere S to the plane P. Lemma If the circle C on S passes through N, then the projection p(C) is parallel to the tangent to C at N. Proof Suppose that C is the intersection of S with the plane F. We know from Theorem 1 that L = p(C) is a line. Now, L, C and T, the tangent to C at N all lie on F. Thus we need only consider this plane. The picture is symmetric about NP, the diameter of C through N, so L and T are perpendicular to this diameter, and hence parallel.
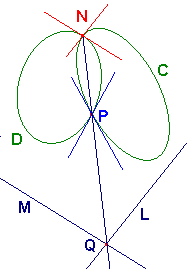
Theorem 2 Stereographic projection preserves angles.
Proof Since the angle between curves on P is defined in terms of tangents, it is enough to consider the case of two lines L and M on P, meeting at Q with angle a. Suppose that these correspond to the circles C and D on S. They meet at P = p-1(Q). Since L and M are lines, C and D also meet in N. By the Lemma, the tangents to C and D at N are parallel to L and M. Thus, the angle between C and D at N is also a. By an earlier remark, the angle beween two circles at both intersections are equal, so the angle between C and D at P is also a.

Stereographic projection