in which the images of the euclidean lines appear as the e-lines. The diagram below
shows how this can be done.
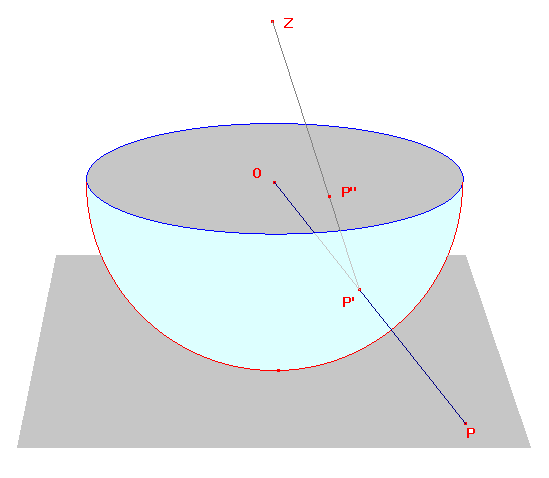
We embed E as the plane z=-1 in R3. We embed D as the disk
x2+y2 < 1, z=0.
O is the origin (0,0,0), Z the point (0,0,1) and S the lower half of the unit sphere,
i.e. S is x2+y2+z2=1, z<0.
Take P on E, and project centrally onto P' on S i.e. P' is where OP meets S.
Now project P' to P" on D using Z, i.e. P" is where ZP' cuts the plane z=0.
We then define a map f from E to D taking P to P". It is clearly bijective.
In the picture, each point for E has the form (x,y,-1), and each point for D
the form (x,y,0) with x2+y2<1. We simply omit the z-coordinates to get a
map f from the plane E to the disk D. We can use real or complex coordinates.
geometrical description
Let L be a line on E, and let S* be the unit sphere centred at O.
The central projection maps L to the circle C on S* where the plane through
L and O cuts S*. This great circle cuts the equator C: x2+y2=1, z=0 in
diametrically opposite points A,B. Now the polar (stereographic) projection
from
S to D maps the arc of C on S to an arc of an i-line through A and B,
i.e. to an e-line. See the stereographic projection page.
algebraic description
theorem
proof
The second, polar, projection maps (x,y,z) (z<0) to (sx,sy,sz+1-s) on the
Composing there two mappings and ignoring the z-coordinate gives f.
Verifying that the inverse is as stated is simply a matter of composing
corollary
proof
If c=0, then L is 2ax+2by=0, which clearly cuts C diametrically.
Thus, we get an e-line in every case.
For (x,y)εE, f(x,y) = (x/(1+A),y/(1+A)), where A = (1+x2+y2)½,
For (x,y)εD, f-1(x,y) = (2x/B,2y/B), where B = 1-x2-y2.
Take P=(x,y,-1). The central projection maps P to P'=(tx,ty,-t) on S.
Hence t2(x2+y2+1) = 1. Also as P' has z< 0, we need the positive root.
Thus, P' = (x/A,y/A,-1/A).
plane z=0. This requires s = 1/(1-z), so we get (x/(1-z),y/(1-z),0).
f with the putative f-1 and checking that the result is the identity.
If K is the euclidean line ax+by+c=0, (a,b)≠(0,0), then f(K) is the e-line
LnD, where L is the i-line c(x2+y2)-2ax-2by-c=0.
Observe that (x,y)εF(K) if and only if f-1(x,y)εK. From the theorem,
this is equivalent to 2ax+2by+c(1-x2-y2) = 0, as required.
If c≠0, then L meets C where 2ax+2by=0, again cutting C diametrically.