- Two distinct e-lines either have the same associated hyperbolic line
(and do not meet in D), or meet exactly once in D. - Given two distinct points A,B, there is exactly one e-line through A and B.
- Given the e-line E and the point A, there is exactly one e-line through A
parallel to E.
For the first part of (1), suppose tha we have two e-lines E=C(P,L) and
F=C(Q,L). If P,Q are on opposite sides of L, then so are E,F, so they
do not meet. If P,Q are on the same side, then eiter P,Q are the same
distance from L, and E,F coincide, or they are at different distances,
and so must be disjoint.
The second part of (1) follows from (2), as we shall see.
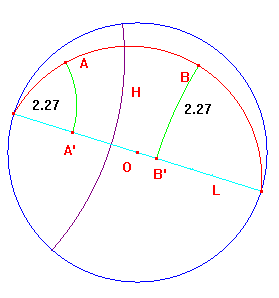
For part (2), let H be the hyperbolic bisector of the segment AB, and
let L be the hyperbolic line through O perpendicular to H. We show that
the e-line E = C(A,L) also passes through B. In the diagram, A',B'
are the feet of the hyperbolic perpendiculars from A,B to L.
Let h denote inversion in H. By the choice of H, h(A) = B.
As H,L are perpendicular, h(L) = L. It follows that h(A') is on L,
and that h(AA') is perpendicular to L. Hence h(A')=B', and so
d(A,A') = d(B,B'). This means that B is on E, so a suitable e-line exists.
Suppose that we take any e-line through A and B. This has the form
F = C(B,L) for some diameter L.
We can use the same diagram, but now
define H as the hyperbolic bisector of A'B', so it is perpendicular to L.
As A,B are on F, d(A,A')=d(B'B'), so ABB'A' is a saccheri quadrilateral
with base A'B', summit AB. By earlier work (which used only the group
of the geometry), H is also the hyperbolic bisector of AB. Since there
is only one diameter L perpendicular to the hyperbolic bisector of AB,
F must be the e-line constructed above.
Now suppose that E,F are e-lines with different associated diameters.
Then it is clear that the e-lines meet. By (2),
if they meet in two points,
then they are identical.
Part (3) was proved in the text.