Proof of Theorem E1
Theorem E1
The group E(2) is generated by reflections.
Proof
Consider the composite s = rM°rL°t.
Thus, each isometry is the composite of (at most three) reflections.
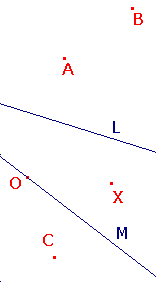
Suppose that t is an isometry, and that t(O)=A, t(X)=B.
As T is an isometry, |AB| = |OX| =1.
Let L be the perpendicular bisector of OA, so rL maps A to O (and vice versa).
Suppose that rL maps B to C. Since the map is an isometry, |OC| = |AB| (= |OX| as above).
Let M be the internal bisector of <XOC. Then rM maps C to X (since |OC| = |OX|).
Considering the effect of each component in turn, we see that s fixes O and X.
By Lemma 1, s is the identity or is rx, reflection in the real axis.
Using the fact that reflections are self-inverse, we have either
t = rL°rM, or
t = rL°rM°rx.