and i-segments. Some of our results can be interpreted as familiar theorems
of euclidean geometry.
Theorem II2
(1) The points A,B,C,D lie on an i-line if and only if (A,B,C,D) is real,
(2) The points C,D lie on the same i-segment AB if and only if (A,B,C,D) > 0.
ratios of the form (u-z)/v-z) for complex numbers u,v and z.
Let U,V,Z be the points with complex coordinates u,v,z.
Then u-z = r.exp(iα), where r = |UZ|, and α is as shown.
and v-z = s.exp(iβ), where s = |VZ|, and β is as shown.
Thus, (u-z)/(v-z) = (r/s).exp(i(α-β), so that
the modulus of (u-z)/(v-z) is the ratio |UZ|/|VZ|, and
the argument of (u-z)/(v-z) is the signed angle VZU.
Now (U,V,Z,W) = ((u-z)/(v-z))/((u-w)/(v-w)), so a determination
of the argument of the cross-ratio is the difference of the signed
angles VZU and VWU.

Theorem A
Suppose that C,D are points not on the line AB.
Then
the points C and D lie on the same arc AB of a circle
if and only if the signed angles BCA and BDA are equal.
This is just a thinly disguised version of Theorem II2(2).
Since C is not on AB, the i-line through A,B and C must
be a circle. The cross-ratio is positive if and only if its
argument is zero. By the remarks just before the theorem,
this is equivalent to the signed angles being equal.
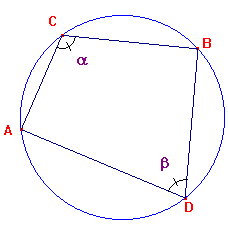
Theorem B
The vertices of a convex quadrilateral ACBD lie on a circle
if and only if the unsigned angles BCA and BDA add to π.
Again, this comes quickly from Theorem II2. Since the quadrilateral
is convex, the vertices would have to lie on opposite arcs of a circle.
From (1) and (2), this happens if and only if (A,B,C,D) is negative.
Thus, the argument of the cross-ratio must be ±π. Let the unsigned
angles be α = <BCA and β = <BDA with α,β in (0,π). Since these
are clearly measured in opposite senses, the signed angles will be
α and -β or -α and β. Either way the difference of the signed
angles will be ±(α+β) so α+β = π.