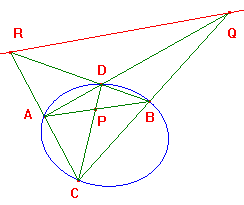
If A,B,C,D are distinct p-points on a p-conic C, and
AB meets CD in P, BC meets AD in Q, and CA meets BD in R,
then QR is the polar of P with respect to C.
Proof
By observation, XY, ZW have equations z = 0 and bx = ay.
By the Three Point Theorem, there is a projective transformation
mapping C to C0 : xy + yz + zx = 0 and A, B, C to the standard
p-points X[1,0,0], Y[0,1,0], Z[0,0,1]. Say it maps D to W[a,b,c],
P to P', Q to Q' and R to R'.
Since a projective transformation preserves the pole/polar
relationship, it is enough to consider the transformed figure.
These intersect in P', so P' = [a,b,0].
By algebraic symmetry, Q' = [0,b,c], R' = [a,0,c].
Using the determinant method, we see that Q'R' has equation
bcx + acy - abz = 0.
As D is on C0, ab + bc + ca = 0, so that -ab = c(a+b).
Then the equation of Q'R' may be written in the form
bcx + acy + c(a+b)z = 0.
As we have a non-degenerate p-conic D is not on XY, so c ≠ 0.
Cancelling c, we get Q'R' : bx + ay + (a+b)z = 0.
By Joachimsthal's Formulae, the polar of P' has equation
½bx + ½ay + ½(a+b)z = 0, i.e. bx + ay + (a+b)z = 0.
Thus Q'R' is the polar of P' with respect to C0.