- The map k is given by k(x,y) = (2x/(1+x2+y2),2y/1+x2+y2)).
- The map k maps the h-line with boundary points AB to the
intersection of the euclidean line AB with D. - The inverse is k-1(x,y) = (x/1+(1-x2-y2)½,y/1+(1-x2-y2)½).
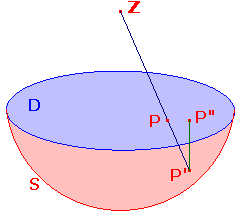
Suppose that (x,y) is in D. This corresponds to P(x,y,0) in R3.
In vector notation, the line ZP has equation tp+(1-t)z = 0,
i.e. each point on ZP has the form (tx,ty,(1-t)), for some t.
This meets S where (tx)2+(ty)2+(1-t)2 = 1, which simplifies to
t2(x2+y2+1) = 2t. The solution t = 0 corresponds to Z. The
other solution, t = 2/(1+x2+y2), corresponds to P'. Thus we have
P' is (2x/(1+x2+y2),2y/(1+x2+y2), 1-2/(1+x2+y2)).
We obtain P" by replacing the z-coordinate by 0.
Thus, we have k(x,y) = (2x/(1+x2+y2),2y/(1+x2+y2)).
For part (2), we show that the points which map to a line segment
lie on an h-line. The point k(x,y) in D is on the line L : ax+by+c = 0
if and ony if 2ax/(1+x2+y2)+2by/(1+x2+y2)+c = 0,
i.e. 2ax+2by+c((1+x2+y2)) = 0.
If c = 0, this reduces to ax+by = 0, i.e.
If c ≠ 0, it is becomes x2+y2-2(-a/c)x-2(-b/c)y+1 = 0.
The distance of O from the line L is d = |c|/(a2+b2)½
Thus, L cuts D if and only if d < 1, i.e.
(-a/c)2+(-b/c)2 > 1.
Using the
Lemma
The circle C : x2+y2-2ax-2by+c = 0 is orthogonal to the circle
C : x2+y2 = 1
if and only if c = 1 and a2+b2 > 1.
we see that the points on L lie on a circle C orthogonal to C.
Since k maps D to D, it maps the h-line
CnD to the segment LnD.
Finally, the map k is defined on the boundary C, and fixes each
point of C -
if P is on C, then P = P' = P" in the definition of k.
Thus, the boundary points ofthe h-line are the end-points of the
segment.
For part (3), we apply the projections in reverse order.
If P" is the point (x,y,0), the orthogonal projection maps it to the
point P'(x,y,z), where x2+y2+z2 = 1 and z < 0.
so z = (1-x2-y2)½.
For brevity, we will use z in our calculations. Then any point ZP'
has the form (tx,ty,tz+1-t). This cuts the xy-plane when t = 1/(1+z),
i.e. at the point (x/(1+z),y/(1+z)), as required.