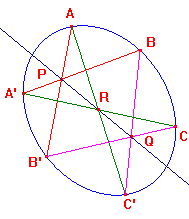
If A,B,C,A',B',C' are distinct p-points on a p-conic C, and
AB',A'B meet in P, BC',B'C in Q and CA',C'A in R, then
P,Q,R are collinear.
Proof
By the Three Points Theorem, we may transform C to the p-conic C0
By inspection :
Then the determinant method gives the following equation for PR :
It is now routine to check that [s,1-s,s(t-1)], the coordinates of Q,
As collinearity is preserved by projective transformation, it is enough
to prove the result for a suitably transformed figure.
with equation xy+yz+zx=0, and A to [1,0,0], B to [0,1,0], C to [0,0,1].
By the Parametrization Lemma, we have constants r,s,t such that
A' = [r,1-r,r(r-1)], B' = [s,1-s,s(s-1)], C' = [t,1-t,t(t-1)].
Note that, since we have distinct p-points, r,s,t ≠ 0,1, and r,s,t distinct.
AB' is sy+z=0, A'B is (1-r)x+z=0, so P = [s,1-r,s(r-1)],
BC' is (1-t)x+z=0, B'C is (s-1)x+sy=0, so Q = [s,1-s,s(t-1)],
CA' is (r-1)x+ry=0, C'A is ty+z=0, so R = [r,1-r,t(r-1)].
(1-r)2(s-t)x + (1-r)s(t-r)y + (1-r)(s-r)z = 0.
Since r ≠ 1, this becomes (1-r)(s-t)x + s(t-r)y + (s-r)z = 0.
satisfy this equation. Thus P,Q,R are collinear.