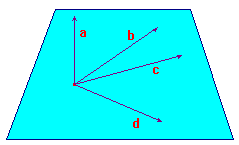
This quantity is very significant geometrically, and admits several interesting
interpretations. The study of this invariant goes back to Greek geometry,
but it looks much more natural in a projective setting.
Suppose that A is a p-point. This is represented by a line through the origin
in R3. If a is a direction vector for this line,
then, as an element
of RP2,
A = [a] . Of course, we could replace
a by a', where a' = λa for any non-zero
real number λ.
Also, a p-line L is represented by a plane Π through the origin in R3. A p-point
A = [a] lies on L if and only if a lies on Π. If B = [b] and C = [c]
also lie on L,
i.e. A,B,C are collinear p-points, then a, b and c lie on Π.
Provided that A ≠ B,
{a, b} is a basis for Π, so that there
exist unique real numbers α and β with
c = αa + βb.
Further, if C ≠ A,B, then
α and β will be non-zero.
Of course, α, β, and even their ratio, will depend upon
the choice of the vectors
a, b and c on their respective lines in R3.
If we introduce a fourth p-point on L, then we do have an invariant.
Suppose that A,B,C,D are distinct collinear p-points, and that a,b,c,d are chosen
so that A=[a], B = [b], C = [c] and D = [d]. Then we have
(1) There exist unique non-zero real numbers α,β,γ and δ such that
c = αa + βb, and d = γa + δb.
(2) The ratio βγ/αδ does not depend on the choice of a,b,c,d.
Of course, part (1) follows easily from the earlier remarks about collinear p-points.
Since the final ratio depends only upon the p-points and not on the choice of
vectors, we can make the
Definition
If A,B,C,D are distinct, collinear p-points then the cross-ratio (A,B,C,D) is the
value of the ratio described in the cross-ratio porism.
Remarks
(2) Since we require that A,B,C,D are distinct, α,β,γ,δ are non-zero.
(3) Since C and D are distinct p-points, (α,β) ≠ λ(γ,δ) for any λ
(4) A cross-ratio can take any value other than 0 and 1.
(1) The value of the cross-ratio will depend on the order of the points.
In the notation of the porism, in calculating (B,A,C,D), we have
c = βb + αa , and d = δb + γa,
so that (B,A,C,D) = αδ/βγ = 1/(A,B,C,D).
The reader may care to verify that we also have (A,B,D,C) = 1/(A,B,C,D).
Thus (A,B,C,D) ≠ 0.
Thus (A,B,C,D) ≠ 1.
To see this, choose c = a+b, and d = λa+b, where λ ≠ 0,1.
The conditions on λ ensure that the p-points A,B,C,D are distinct.
Then (A,B,C,D) = 1.λ/1.1 = λ.
Suppose that t is a projective transformation. Then t maps p-lines to p-lines.
Thus, if A,B,C,D are collinear p-points, then t(A),t(B),t(C),t(D) are also collinear,
so their cross-ratio is defined. We shall write t(A,B,C,D) for (t(A),t(B),t(C),t(D)).
The projective cross-ratio theorem
Cross-ratio is invariant under the projective group P(2).
It is often useful to note that, if A,B,C lie on a p-line L, then there is a unique
p-point D on L with a given value of (A,B,C,D). The uniqueness is guaranteed by
Theorem PI1
If A,B,C,D,E are collinear p-points such that (A,B,C,D) = (A,B,C,E), then D = E.
To use this invariant to obtain euclidean results, we need to consider
embeddings of RP2.