We have looked at several geometries, and have established relationships between the defining groups. At the start, we showed that such relationships implied that the properties and congruence classes were related. In particular, the theorems of the geometry of a group can be interpreted as theorems of any geometry defined by a subgroup. For examply, the Medians Theorem is a result in affine geometry, so is a theorem of euclidean geometry.
We also showed that the similarity group S(2) is a subgroup of the inversive group I(2). In fact, S(2) consists of elements fixing ∞, i.e. S(2) = S({∞),I(2)). This defines similariy geometry on the set obtained by removing ∞. Observe that elements of S(2) map i-lines through ∞ only to i-lines through ∞. Thus the family of i-lines splits in this geometry. The lines of similarity geometry come from the i-lines through ∞, with ∞ deleted. Thes are, of course the euclidean lines in the familiar plane model. We defined the hyperbolic group H(2) as the subgroup of I(2) consisting of the elements mapping the disk D to itself, i.e. H(2) = S(D,I(2)). This is a subgroup of S(C,I(2)), the inversive symmetry group of the unit circle C. The subgroup H(2) defines a geometry on D. But, we do not define the lines of the geometry as all the non-empty sets LnD , where L is an i-line. Observe that inversion in an i-line L maps D to itself, i.e. belongs to H(2), if and only if L is orthogonal to C. The h-lines are the intersections LnD for such i-lines L. One of the key features of inversive geometry is the property of angle. Thus similarity (and hence euclidean) and inversive geometries inherit the property of angle. In iversive geometry, the i-lines include all circles and lines. In similarity geometry, those which do not include ∞, i.e. the circles form a single conjugacy class. In euclidean geometry, this class splits into infinitely many classes, diferentiated by a property we christen "euclidean length". In the hyperbolic case, a circle within D must map to another such circle. Such circles are called hyperbolic circles.Again, these fall into infinitely many classes. The distinguishing property is called "hyperbolic length". Indeed, this is the way we defined the hyperbolic length. Problems involving circles in these geometries are often consequences of results from inversive geometry. For example, in inversive geometry, there is a unique i-line through any three points. In euclidean geometry, the i-line may give a line or circle. We can state this as Given three points in the plane, either the points are collinear or they lie on a unique circle. In hyperbolic geometry, the i-line may be neither orthogonal to C nor within D, so lie on at most one h-line or hyperbolic circle.
We saw that E(2) < S(2) < A(2) , relating euclidean, similarity and affine geometries. We also showed that A(2) is isomorphic to a subgroup of P(2).In detail, we showed that A(2) is isomorphic to the subgroup of P(2) fixing the p-line Z : z=0, i.e. to the projective symmetry group of Z, S(Z,P(2)). The elements of S(Z,P(2)) map p-points on Z to other p-points on Z. The subgoup therefore defines a rather trivial geometry on the set Z. On the other hand, for p-points P,Q not on Z, then there is an element of S(Z,P(2)) mapping P to Q. Thus the subgroup defines a geometry on the rest of the projective plane. We get a nice model by observing that a p-point not on Z meets the plane Z* : z=1 in a unique point. The restrictions to Z* give the usual model of affine geometry. If L and M are p-lines other than Z, then they define lines of affine geometry. As p-lines, they meet in a p-point R. If this is not on Z, the affine lines do meet. If R is on Z, then the affine lines do not meet. This explains the appearance of the concept of parallelism in affine and hence in euclidean geometry. Indeed, the model can be used to prove the fundamental result which we shall call The Parallel Theorem If L is a line in affine geometry and P is a point not on L, then there is a unique line through P not meeting L. proof
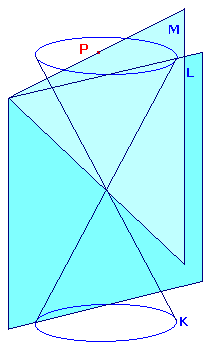
We have shown that the hyperbolic group H(2) is isomorphic to a subgroup of P(2). Although we could use any conic to obtain this result, we chose the minkowsi model since this is related to special elativity. The conic is K : F(x,y) = x2+y2-z2 = 0. Then H(2) is isomorphic to S(K,P(2)). We obtain the model be looking at the positive sheet of the hyperboloid H : F(x,y) = 1. The hyperbolic lines correspond to the intersections of H with the p-lines which actually cut H.Given a p-line L and a p-point P inside K, there are many p-lines M through P (and hence cutting H) which meet L outside K. The limiting positions of this collection are those joining P to the p-points where the p-line L meets K. Thus, we see that there is no Parallel Theorem here. The sketch on the right shows the cone K and a p-line M through P which meets L outside K. The principal features of projective geometry are incidence (including tangency) and cross-ratio. Provided that we take care about p-points of RP2 which do not give rise to affine or hyperbolic points, we get corresponding results for these geometries. For example, we have in either geometry Pappus's Theorem Suppose that points A,B,C lie on a line L, and A',B',C' on a line L' and that AB',A'B meet in P, BC',B'C in Q, and CA',C'A in R, then P,Q,R are collinear. The italicised condition is vital, ther will be cases where the lines fail to meet. In affine (and hence euclidean) geometry, lines which fail to meet are parallel, so we can recover variants for such cases. As an example, we have Euclidean Variant Suppose that points A,B,C lie on a line L, and A',B',C' on a line L' are such that AB'and A'B are parallel, and BC'and B'C are parallel, then CA',C'A are parallel. This is easy to see in the projective setting. Two euclidean lines are parallel corresponds to the statement that they meet at an ideal point. If AB',A'B and BC',B'C are parallel, then they meet at points on the ideal line. From the projective version of Pappus, CA',C'A also meet at an ideal point, so that the euclidean lines are parallel.

main klein page