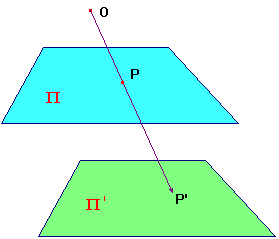
If Π and Π' are planes in 3-dimensional space,
and O is a point which lies on neither plane, then
the perspectivity from Π to Π' with vertex O,
is the map t which maps P on Π to P' on Π',
the point where OP cuts Π' (if it exists).
In our initial discussions, we consider only the cases
where Π and Π' are non-parallel. These provide clear
motivation for the extension to extended planes. The
parallel case is easier, and is dealt with at the end.
Shortly, we will see why the proviso is needed in general.
Note that, whatever plane Π' is chosen, P' (if it exists)
will lie on the line OP.
Note also that, if we reverse the roles of Π and Π',
then we get a map taking P' to P, i.e. t-1 is the
perspectivity from Π' to Π with vertex O.
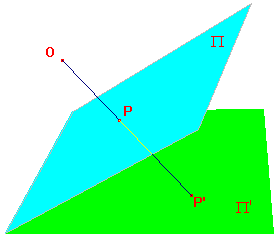
Let Π* denote the plane through O, P and Q.
For any point R on the line PQ, the line OR will lie on Π*.
It follows that the image of R (if it exists) will lie on the
the line of intersection of Π* and Π'.
In this case, the line PQ maps to a line on Π'.
We assumed that the line PQ was such that the plane Π*
met Π'. Of course, for some choices of P and Q, we will
have Π* = OPQ parallel to Π'. This will happen precisely
when P and Q lie on the line L where Π meets the plane
through O parallel to Π'.
This is discussed in the next pargraph.
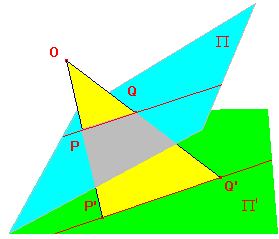
For P not on L, OP is not parallel to Π', so meets Π'.
For R on L, OR is parallel to Π', so t(R) cannot be
defined as the intersection of OR and Π'.
To see how we can define t(R), we first consider
the family of lines on Π passing through R other than L.
Since each such line is not parallel to Π', its image is
a line on Π'. Since two such lines meet only in R,
and R has no image, the images do not meet on Π'.
Thus, the images are a family of parallel lines on Π'.
When defining extended planes, we defined an ideal point
for Π' as a new "point" added to each member of a family
of parallel lines. Thus, we say that t(R) is the ideal point
of Π' defined by the family of images.
Since each point of L maps to an ideal point of Π', this
means
that the image of L itself is the ideal line of Π'.
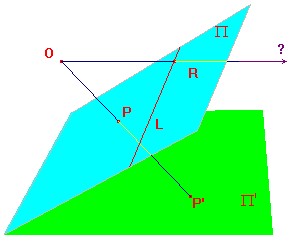
there is a line L' on Π' mapped by t-1 to the ideal line of Π.
It follows that the ideal line of Π should have image L'.
We now have a bijection from the extended plane Π to
the extended plane Π'. We still denote it by t, and refer
to it as a perspectivity.
Then for any P on Π, OP meets Π', so t(P) is always
defined as a point of Π', and each point of Π' arises
in this way.
The image of a family of parallel lines on Π will be
a family of lines on Π'. The latter family will also be
parallel, since any intersection would be the image of
a point on Π, and this would lie on the original family.
Thus t may be said to map the ideal points of Π to
those of Π'. Again we have a map of the extended
planes.
In fact, the perspectivities generate P(2), as we shall see.