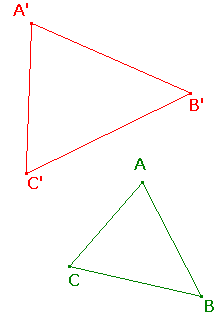
The Scaling Theorem A similarity scales all distances by a fixed positive factor. Proof Suppose that A and B are distinct points on the plane. Suppose first that C is not collinear with A and B. Let the similarity s map A, B, C to A', B', C' respectively. Since s preserves the size of angles, triangles AB and A'B'C' are similar, so the ratio of corresponding sides are equal, e.g. A'C'/AC = A'B'/AB = k, say. Now suppose that D is on the line AB. By considering the effect of s on triangle ACD, we see that A'D'/AD = A'C'/AC. But A'C'/AC = k, by the previous case, so A'D'/AD = k. Thus s scales all segments from A by the factor k = A'B'/AB. Similarly, s scales all segments from B by this factor. Since A and B were arbitrary, s scales all distances by the same factor.

Corollary Each similarity can be written as the composite of an isometry and a dilation about O. Proof Let s be a similarity. By the Theorem, s scales all distances by a factor k > 0. Note that sk (scaling about O with factor k) has inverse s1/k. Then t = s°s1/k scales distances by factor k.(1/k) = 1, i.e. is an isometry. Thus s = t°sk, as required.

similarity group page