Suppose that C and C' are p-conics, and that A lies on C, and A' on C'.
(a) If P lies inside C, and P' inside C',
then there are precisely two projective transformations which map
C to C', A to A', and P to P'.
(b) If P lies outside C, but not on the tangent to C at A, and
P' lies outside C', but not on the tangent to C' at A',
then there are precisely two projective transformations which map
C to C', A to A', and P to P'.
proof
(1) P outside C.
(2) P inside C.
Since the chord RS is constructed using the ideas of polar and pole, the
Let R'S' be the chord of C' associated with A',P'.
If t is as in the statement of the theorem, then the above remarks show
If, conversely, t maps C to C', A to A', and {R,S} to {R',S'}, then, since
In case (b), the restriction that P, P' are not on the tangents at A, A'
We have reduced the problem to that of finding transformations which map
Although there are differences in detail depending on whether P and P' lie
inside or outside their respective p-conics, the basic idea is the same. We
associate with the pair A,P a chord RS of C in such a way that P can be
recovered from A and the chord RS. Likewise, with A',P', we associate the
chord R'S'. We show that any suitable projective transformation must map
RS to R'S' . Since A,R,S lie on C and A',R'S' on C', the three point theorem
can be applied provided the triples consist of distinct p-points.
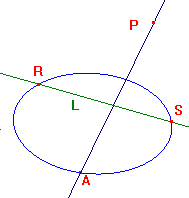
From our definition of outside, the polar of P with respect to C cuts C twice.
Let the intersections be R and S. Here, RS does not depend on A.
Suppose that we are given the chord RS, then we recover P as the pole of
the p-line RS.
But note that, if P is on the tangent at A, then A = R or A = S.
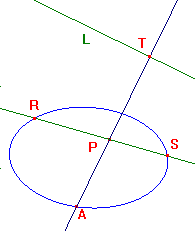
Let L be the polar of P with respect to C, and T the p-point where L meets
the p-line AP. As P is inside C, L does not meet C, so T is outside C. Thus,
the polar of T with respect to C cuts C twice, at R,S, say. Once again, we
have a chord RS associated with A,P. This time, it does depend on A. Note
that, as T lies on the polar of P, La Hire's theorem shows that P lies on the
polar of T, i.e. on RS. Thus P is the intersection of AT and RS.
Suppose that we are given the chord RS, and the p-point A. We recover T
as the pole of the p-line RS. Then we recover P as the intersection of the
p-lines AT and RS.
invariance theorem shows that, if t is any projective transformation,
then t(RS) will be the chord of t(C) associated with t(A), t(P).
that t(RS) = R'S', i.e. {R,S} maps to {R',S'} as sets.
A, RS determine P, and A', R'S' determine P', t maps P to P'.
ensure that A,R,S and A'.R',S' are distinct triples.
C to C', A to A' and {R,S} to {R',S'}. The last condition can be satisfied in
two ways - we can map R to R' and S to S' or R to S' and S to R'. Finally, we
invoke the three points theorem which shows that there is exactly one map
of each type. Thus, we have precisely two suitable transformations.