

|
Suppose that C and D are distinct conics.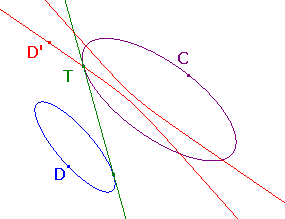 The Common Tangents Theorem
The Common Tangents Theorem
Then the common tangents (if any) to D and C
occur at the points
where C intersects the dual of D with respect to C.
Proof
Let D' be the dual of D. Then, of course, D is the dual of D'.
Suppose first that D' meets C at T.
Suppose now that there is a common tangent L to C and
D, meeting C at T, say.
Throughout the proof duality means duality with respect to C.
As T is on C, the dual of T is the tangent to C at T.
As D is the dual of D', the dual of T is a tangent to D,
so is a common tangent to C and D.
As L is the tangent to C at T, T is the dual of L.
As L is also a tangent to D, T, the dual of L, must lie on D', the dual of D.
Thus T lies on the intersection of C and the dual of D.
| Geometry Page |