Some results on quadrilaterals

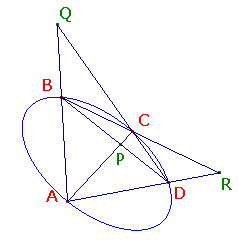
The Inscribed Quadrilateral Theorem
If the vertices of a quadrilateral lie on a conic,
then the line joining the intersections of opposite sides
is the polar of the intersection of the lines joining opposite vertices.

Proof of the Inscribed Quadrilateral Theorem

This suggests a construction for the polar of a point P:
Take two lines through P, meeting the conic at A,B,C and D.
Then the polar of P is the line joining the intersections of AB,CD and of AD,BC.
Unfortunately, this will fail if P lies on the conic (when it should return the tangent).

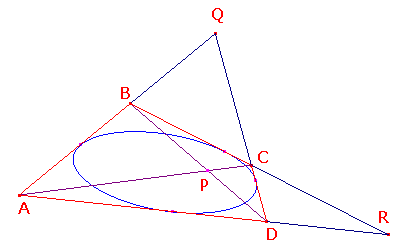The dual of this is

The Circumscribed Quadrilateral Theorem
If the sides of a quadrilateral touch a conic,
then the intersection of the lines joining opposite vertices
is the pole of the line joining the intersections of opposite sides.

Here, we may observe that to say that a point P is the pole of a line QR
is exactly the same as saying that QR is the polar of P.
Then we see that the two theorems assert the same property
for the quadrilateral, viz

If a quadrilateral is inscribed in, or circumscribed round a conic,
then the line joining the intersections of opposite sides is
the polar of the inersection of the diagonals.

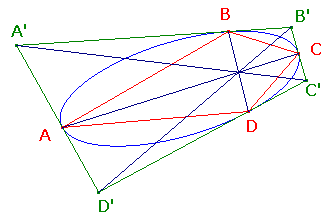
Indeed, corresponding inscribed and circumscribed quadrilaterals
have the following remarkable property.
I have chosen the name since it involves two quadrilaterals,
each of which is the dual of the other.

The Dual Quadrilaterals Theorem
If the quadrilateral ABCD is inscribed in a conic, and the
tangents at A,B,C,D (in order) define the circumscribed quadrilateral A'B'C'D', then the diagonals of the quadrilaterals are concurrent.

Proof of the Dual Quadrilaterals Theorem