Notation
For a given point P,
tP denotes the isotomic conjugate of P,
T(P) denotes the tripolar of P,
I(P) denotes the inconic with perspector of P,
C(P) denotes the circumconic with perspector P.
X* denotes the P-Ceva conjugate of X.

We will use the numbering of ETC where possible.

Points on inconics

An inconic is characterized by the fact that the sidelines are tangents. It is therefore reasonable
to think of an inconic as a line-locus rather than a point-locus. From a projective point of view,
it would be possible to describe the inconic I(P) as the dual of the circumconic C(tP). In triangle
geometry, it is more sensible to view I(P) as the line-locus {T(X) : X on T(P)} since the concept
of tripolar arises naturally. We can recover the point of contact quite easily.

Theorem 1
Suppose that X lies on T(P). Then the line T(X) touches I(P) at X* ( the P-Ceva conjugate of X).

This is easy to verify. If X = x:y:z and P = p:q:r, and X on T(P), X* = x²/p:y²/q:z²/r.
As X is on T(P), X* is on T(X), and on I(P). That T(X) touches I(P) is easily checked by algebra.

Notes :
(1) As P-Ceva conjugation is an involution, we can use this map to recover X from X*.
(2) We can often obtain X* directly as an intersection of lines - see below.

This can be rephrased as follows :

Corollary 1.1
The inconic I(P) is the image of T(P) under P-Ceva conjugation.
If X is on T(P), then T(X) is the tangent to I(P) at X*.

Note :
For X on T(P), the point X* can be described variously as the
cevian quotient (P-Ceva conjugate) of P and X,
cevian product (cevapoint) of P and X,
image of P under the isoconjugation fixing X.
The last gives the simplest algebra, as in Theorem 1.

Algebra
Observe that a point X on T(P) has barycentrics pu:qv:rw, with u+v+w = 0.
Then, from Theorem 1, X* on I(P) has coordinates pu²:qv²:rw².
The point u:v:w is on the Line at Infinity, but we do not view it as significant.

If X is on T(P), then X* is on I(P). The line X-X* will meet I(P) again. We can identify
geometrically the point Y on T(P) for which Y* is this second intersection.

Theorem 2
Suppose that X is on T(P), and that Y is the intersection of T(P) and T(X).
Then X, X* and Y* are collinear (so Y* is the second meet of X-X* and T(Y)).

This is easy to verify, even by hand, once we evaluate the coordinates of Y.
Note that it is best to find Y* and then check that X is on the line X*-Y*.

Algebra
For X on T(P), let X have coordinates pu:qv:rw, with u+v+w = 0, the point Y has the
form pu(v-w):qv(w-u):rw(u-v). This can be rewritten p(1/v-1/w):q(1/w-1/u):r(1/u-1/v).

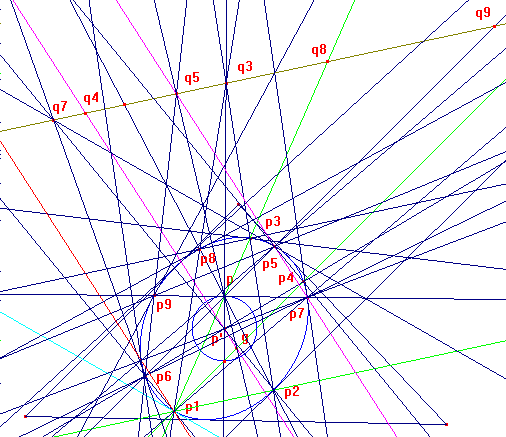
Eleven basic points on an inconic

We now describe some points on the inconic I(P) derived in this way.

Note : all are obtained by line intersections, no conic operations are used.

Let P' denote the centre of the inconic I(P).

Summary
We know that each point of I(P) is associated with a point of T(P) using P-Ceva conjugation.
The most obvious point on T(P) is its infinite point Q1. This leads to our first point P1 on I(P).
Theorem 2 immediately gives another as that on the line P1-Q1. This is the point P2. More
generally, for any point W not on I(P), there will be a second point on I(P) and the line P1-W.
Taking W = P, P', G, we construct P3, P4, P5. The other points are derived from the earlier ones.

Detail
Let Q1 be the infinite point on T(P).
Let P1 = Q1*.
This can be constructed as the intersection of T(Q1) with the tripolar of the isotomic
conjugate of the tripole of G-P (this is also the tripolar of the infinite point of T(tP)).
Note :
P1 is the contact with the fourth common tangent of I(P) and the Stelner Inellipse,
this tangent being the line T(X1).

Let Q2 be the intersection of T(P) and T(Q1).
Let P2 = Q2*.
This can be constructed as the intersection of T(Q2) with the line P1-Q1,
i.e. the parallel to T(P) at P1.
Notes :
Q2 is the tripolar centroid of P;
T(Q1), T(Q2) and P-P' are concurrent.

Let Q3 be the intersection of T(P) and the line P-P'.
Let P3 = Q3*.
This can be constructed as the intersection of T(Q3) with the line P1-P.
Notes :
P3 is on the line P1-P, by construction:
T(Q3), T(Q1) and T(P) concur at Q2;
P2, P3, Q3 collinear.

Let Q4 be the intersection of T(P) and the line G-P'.
Let P4 = Q4*.
This can be constructed as the intersection of T(Q4) with the line P1-G.
Note : T(Q1), T(Q4) and T(tP) concur.

Let Q5 be the intersection of T(P) and the line G-P.
Let P5 = Q5*.
This can be constructed as the intersection of T(Q5) with the line P1-P'.
Note : P5 is the antipode of P1, so T(Q1) and T(Q5) are parallel.

There is a sixth related point on the inconic. We can check that the lines P-P5 and P'-P4
meet at a point P6 on I(P). Of course, P6 is the antipode of P4, as P' is on P4-P6. Also,
the tangents at P5 and P6 meet on T(P) as the polar of P in I(P). The point P6 must be
Q6* for some Q6 on T(P). We can construct this in various ways. For example, let L be
the tripolar of the isotomic conjugate of the complement of P. The line L meets T(P) at
the required Q6.
Notes :
T(P), T(Q5) and T(Q6) concur at a point Q7;
T(Q1), T(Q4) and P'-Q7 concur;
P1,P4,P5,P6 is a parallelogram since P', the centre of I(P), is on P1-P5 and P4-P6.

This Q7 allows us to define a seventh point P7 = Q7* on I(P).
Notes :
P5, Q5 and Q7 are collinear;
P6, Q6 and Q7 are collinear;
Q7, P' are collinear with the intersection of T(Q1) andT(Q4).

Let Q8 be the intersection of T(P) and the line P1-P3.
Let P8 = Q8*.
This can be constructed as the intersection of T(Q8) with the line P2-P.
Notes
P8 is on P3-Q1 and on P1-Q3 as well as P2-P;
T(Q2),T(Q8) and T(P) concur.

Let Q9 be the intersection of T(P) and the line P5-P6.
Let P9 = Q9*.
This can be constructed as the intersection of T(Q9) with the line P7-P.
Notes
P9 is on P5-Q6 and on P6-Q5 as well as P7-P;
T(Q7),T(Q9) and T(P) concur.

We can derive further points using pairs Pm, Pn with P on Pm-Pn; see Construction 6.
This yields a further pair of points on I(P) with P on the chord so we can continue.

Example : m = 2, n = 8.
Let Q10 be the intersection of T(Q2) and T(Q8) - this is on T(P).
Let P10 = Q10*.
This is the intersection of P2-Q2 and P8-Q8.
Note : T(Q2),T(Q9) and T(P) concur.
Let Q11 be the intersection of T(P) and the line P2-P8.
Let P11 = Q11*.
This can be constructed as the intersection of the lines P2-Q8 and P8-Q2.
Notes :
P is on the line P10-P11;
T(Q10),T(Q11) and T(P) concur.

Some examples

inconic	perspector P	point P1
incircle	X7	X11
Mandart	X8	X11
orthic	X4	X125
unnamed	X69	X125
unnamed	X3	X2972
Macbeath	X264	X2972
Kiepert	X99	X1649
unnamed	X523	X1649

These illustrate the following result :

Theorem 3
The inconics with perspectors P and tP have the same point P1.

The proof is trivial algebra.

Pairs of points on an inconic

Suppose that W is a fixed point not on an inconic I(P), and that X is any point on I(P).
Then the line WX meets I(P) again at another real point Y (which may be X again).

Here, we describe how pairs such as X and Y may be obtained.

Theorem 4
Suppose that W is a fixed point not on I(P).
Let X be any point on T(P).
Let Y be the intersection of T(P) and the tripolar of the cevapoint of W and X.
Let X* and Y* be the P-Ceva conjugates of X and Y.
Then X* and Y* lie on I(P), and W on the line X*-Y*.

Proof
By the general theory, X* and Y* lie on I(P).
Maple shows that W, X* and Y*are collinear.

There are several instances above. For example, with W = P, X = Q1, the tripolar is the
line P-P', so that Y is Q3. We have observed that P3 is on P1-P.

Special Case
When we take W = P, the algebra is relatively simple. Let X = pu:qv:rw, with u+v+w = 0.
Then X is on T(P), and X* = pu²:qv²:rw². In this case, the second intersection of I(P) with
the line P-X* derives from the point X' = p(v-w):q(w-x):r(u-v) on T(P).

Other cases
For these, we give the barycentrics of the point X' on T(P) giving the second meeting of I(P)
with W-X*, where X = pu:qv:rw.

W = P' X' = p(qv-rw):q(rw-pu):r(pu-qv),
W = G, X' = p(f(q,r,p)v-f(r,p,q)w):q(f(r,p,q)w-f(p,q,r)u):r(f(p,q,r)u-f(q,r,p)v),
where f(x,y,z) = 1/p-1/q-1/r.

Three points on I(P) from a point on T(P)

We first show how we can associate three points on I(P) with each point X on T(P).
Some simple algebra shows that, for X on T(P), the polar of X meets I(P) in real points.

Remark.
This result was discovered by Cabri sketching. It can be verified by algebra.
The construction involves intersecting a line with a conic, and it appears that
the points S2,S3 (or R2,R3) cannot be obtained by line intersections alone.

Theorem 5
Suppose that R1 is a point on T(P).
Then there are points S1, S2, S3 on I(P) such that
(1) T(R1) is tangent to I(P) at S1.
(2) The tangents at S2, S3 meet at R1.
(3) P is on the line S2-S3.
(4) S1 is the intersection of R2-S2 and R3-S3 (where Ri = P-Ceva conjuagte of Si).

Proof
By the above theory, S1, the P-Ceva conjugate of R1, is on I(P).
Also, S1 is the contact point of T(R1) with I(P).
Now let T2, T3 be the tangents to I(P) from R1.
Let the contact points be S2, S3, respectively, so these are on I(P).
As T(P) is the polar of P with respect to I(P), P is on the line S2-S3.
Let R2, R3 be the P-Ceva conjugates of S2, S3.
By the above theory, the lines T(R2), T(R3) are the tangents T2, T3.
By computation, the lines R2-S2 and R3-S3 both pass through S1.

Examples
S1 = P2, {S2,S3} = {P1,P3},
S1 = P7, {S2,S3} = {P5,P6}.

We could equally derive this structure starting from S2 (or S3). This is in the next section.

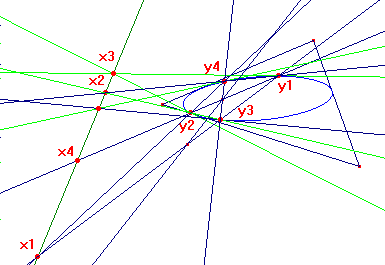
Four points from a point on I(P)

Suppose that X1 is a point on I(P). We construct three further points on I(P) as follows.

Construction 6
Stage 1
This is the construction of the second intersection of X1-P with I(P).
See the Special Case of Theorem 4.

Let Y1 be the P-Ceva conjugate of X1, so Y1 is on T(P), and X1 on T(Y1).
Let Y2 be the intersection of T(P) and the tripolar of the cevapoint of P and Y1.
Let X2 be the intersection of T(Y2) and the line P-X1.

Stage 2
This constructs two related points X3, X4 with P on X3-X4.
Let Y3 be the intersection of the tripolars T(X1) and T(X2). This lies on T(P).
Let X3 be the intersection of the lines X1-Y1 and X2-Y2. This lies on I(P).
Let Y4 be the intersection of T(P) and the line P-X1.
Let X4 be the intersection of T(Y4) and the line P-X3.
We can obtain X4 directly as the intersection of the lines X1-Y2 and X2-Y1.

There is some symmetry. Clearly, we get the same points starting from X2 instead of X1.
However, although X3, X4 are also collinear with P, they do not give the same quartet.
It follows that we can repeat Stage 2 with X3, X4 instead of X1, X2.

Collinearities :
Y1, X1, X3,
Y1, X2, X4,
Y2, X1, X4,
Y2, X2, X3,
P, X1, X2,
P, X3, X4,
P, Y1, T(X1)nT(X4), T(X2)nT(X3),
P, Y2, T(X1)nT(X3), T(X2)nT(X4).

Concurrences :
T(P), T(X1), T(X2) (at Y3),
T(P), T(X3), T(X4).

Conics
The inconics I(X1), I(X2) also pass through X3.
The circumconic C(Y3) touches
X1-X2 at P,
X1-X3 at Y1,
X2-X3 at Y2.
For n = 1,..4, C(Xn) touches T(P) at Yn.

Algebra
We know that a pair {Y1,X1} with Y1 on T(P), X1 on T(Y1) and I(P) have the forms
Y1 = pu:qv:rw, X1 = pu²:qv²:rw², with u+v+w = 0.
We give the multipliers of p, q, r for each Yn.

Y1 : u:v:w,
Y2 : v-w:w-u:u-v
Y3 : 1/v-1/w:1/w-1/u:1/u-1/w,
Y4 : 2/u-1/v-1/w:2/2-1/w-1/v:2/w-1/u-1/v.

We can view the coordinates in line 3 as the product of those in lines 1 and 2.
We can view the coordinates in line 4 as V-W:W-U:U-V, where U:V;W as in line 3.

Warning : In this sketch, the labels Xn and Yn are reversed.

Infinite sequences of points on an inconic

Suppose we have a pair {X,X*} with X on T(P), X* on I(P) as above. We get another point on
I(P) as the intersection of X-X* with the line T(Y), where Y is the intersection of T(P) and T(X).
By Theorem 2, this is the point Y*. We now have a second pair {Y,Y*}. We can repeat this to
get an infinite sequences of points on T(P) and on I(P).

Note :
After the initial step, which uses P-Ceva conjugation, only line intersections are needed.

The sequences {X(n)} on T(P) and {X*(n)} on I(P) are given by
X(1) a point on T(P),
X*(1) the P-Ceva conjugate of X(1),
X(n+1) the intersection of T(X(n)) and T(P),
X*(n+1) the intersection of X(n)-X*(n) and T(X(n+1)).

Note that we could define X*(n) as the P-Ceva conjugate of X(n) in general.
We can easily find the coordinates, but they do not appear very interesting.

Appendix - coordinates for Qn, Pn, n = 1...9.

The points Qn, Pn have coordinates Qn = px:qy:rz and Pn = px²:qy²:rz², with
Rn = x:y:z at infinity. For brevity, we list the first coordinate of each Rn.

n	u(n) = first coordinate
1	q-r
2	(q-r)(2p-q-r) = (r-p)2-(p-q)2 = 1/(r-p)-1/(p-q)
3	(2p-q-r)
4	q2(r-p)-r2(p-q)
5	(2/p-1/q-1/r)
6	(1/q-1/r)
7	(1/q-1/r)(2/p-1/q-1/r)
8	2(q-r)2-(r-p)2-(p-q)2
9	2(1/q-1/r)2-(1/r-1/p)2-(1/p-1/q)2
more complicated coordinates .......
10	u(2)u(8)
11	v(10)-w(10)

main index