Low-dimensional topology on Skye

Format and other details

• This will be a Banff-style workshop. Accommodation and meals onsite will be provided. We will also provide a coach from Glasgow to Skye and back (details below).
  Some funds for travel to Glasgow may be available for those who require them.
  A schedule of talks will be posted shortly before the beginning of the workshop.

Travel to Skye

• We have booked a coach which will take participants from Glasgow to Skye on Sunday 11th June. It will depart from Wolfson Medical Building, University Avenue at 3:30pm and will then make a stop at Glasgow Airport (turn right out of terminal building for coach park) at 4pm. There will be a refreshment stop for about 45 minutes at Fort William at around 6:30pm, which will give a chance to get some food. We expect to arrive at SMO around 9:30pm.
  The return coach will leave Skye for Glasgow after breakfast on Saturday 17th June. We expect to arrive at Glasgow Airport between 3pm and 4pm.
  Alternatives: if the coach does not suit you, you may consider renting a car and driving; or taking the train from Glasgow Queen St, to connect with the Mallaig-Armadale ferry. The train and ferry timetable is here. From certain locations it may be possible to take a train to Kyle of Lochalsh, which is within taxi distance from the conference. For train times in the UK see http://www.nationalrail.co.uk.
  For more useful information on travel to Skye, such as where to land your helicopter, try this link, which is from the web page of a different conference.

Schedule

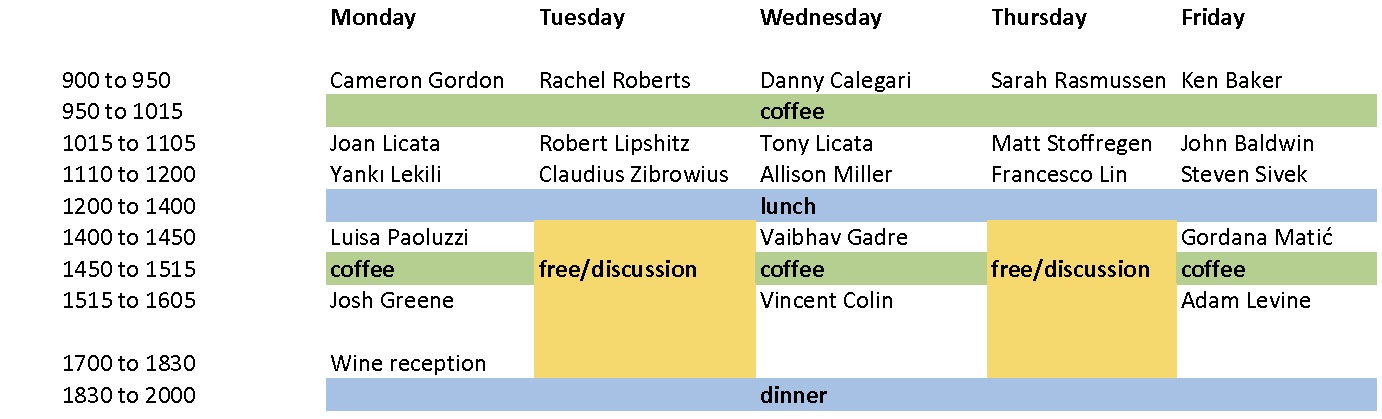
(Titles and abstracts below)

Participants

• Paolo Aceto, Renyi Institute
• Ken Baker, Miami
• John Baldwin, Boston College
• Hans Boden, McMaster
• Steve Boyer, UQàM
• Danny Calegari, Chicago
• Vincent Colin, Nantes
• Vaibhav Gadre, Glasgow
• Cameron Gordon, Texas
• Josh Greene, Boston College
• Chris Herald, UNR
• Kyle Larson, MSU
• Yankı Lekili, KCL
• Adam Levine, Princeton
• Joan Licata, ANU
• Tony Licata, ANU
• Francesco Lin, Princeton
• Robert Lipshitz, Oregon
• Andrew Lobb, Durham
• Joseph MacColl, UCL
• Gordana Matić, Georgia
• Irena Matkovič, CEU
• Duncan McCoy, Texas
• Allison Miller, Texas
• Matthias Nagel, McGill
• Brendan Owens, Glasgow
• Luisa Paoluzzi, Marseilles
• Lisa Piccirillo, Texas
• Sarah Rasmussen, Cambridge
• Rachel Roberts, WSUL
• John Shareshian, WSUL
• Steven Sivek, MPIM
• Mike Snape, Glasgow
• András Stipsicz, Renyi Institute
• Matthew Stoffregen, UCLA
• Sašo Strle, Ljubljana
• Daniel Waite, Glasgow
• Andy Wand, Glasgow
• Liam Watson, Glasgow/Sherbrooke
• Claudius Zibrowius, Cambridge

Talks

• Monday June 12
  
  Left-orderability, foliations, L-spaces and cyclic branched covers, Cameron Gordon
  It has been conjectured that for a prime 3-manifold M the following are equivalent: (1) π₁(M) is left-orderable, (2) M admits a co-orientable taut foliation, and (3) M is not a Heegaard Floer L-space. We will discuss these properties in the special case where M is the n-fold cyclic branched cover of a knot.
  
  Morse Structures on Open Books, Joan Licata
  Every contact 3-manifold is locally contactomorphic to the standard contact R³, but this fact does not necessarily produce large charts that cover the manifold efficiently. I'll describe joint work with Dave Gay and more recently, Dan Mathews, which uses an open book decomposition of a contact manifold to produce a particularly efficient collection of such contactomorphisms, together with simple combinatorial data describing how to reconstruct the contact 3-manifold from these charts. We use this construction to define front projections for Legendrian knots and links in arbitrary contact 3-manifolds, generalising existing constructions of front projections for Legendrian knots in S³ and universally tight lens spaces.
  
  Mirror symmetry for punctured surfaces and Auslander orders, Yankı Lekili
  We consider partially wrapped Fukaya categories of punctured surfaces with stops at their boundary. We prove equivalences between such categories and derived categories of modules over the Auslander order on certain nodal stacky curves. As an application, we deduce equivalences between derived categories of coherent sheaves (resp. perfect complexes) on such nodal stacky curves and the wrapped (resp. compact) Fukaya categories of punctured surfaces of arbitrary genus. This is joint work with Polishchuk.
  
  Features of knots that are sometimes related to the presence of symmetries, Luisa Paoluzzi
  Symmetric knots are obviously special. After recalling what symmetries are and presenting some basic properties, I will survey three types of situations in which the presence of symmetries may be related to other characteristic of the knot, namely its behaviour with respect to orientations, to cyclic branched cover, and to the fact of being trivial.
  
  (1,1) L-space knots, Josh Greene
  I will prove and discuss a characterization of (1,1) L-space knots in joint work with Sam Lewallen and Faramarz Vafaee.
  
  
• Tuesday June 13
  
  Constructing CTFs, Rachel Roberts
  I will describe a construction of (codimension one) co-oriented taut foliations (CTFs) of 3-manifolds. It follows from this construction that if K is a composite, alternating, or Montesinos knot, then the L-space conjecture of Ozsváth and Szabó holds for any 3-manifold obtained by Dehn surgery along K. This work is joint with Charles Delman.
  
  Bordered involutive Floer homology, Robert Lipshitz
  Hendricks-Manolescu introduced involutive Heegaard Floer homology as a partial analogue of pin-equivariant monopole Floer homology. We will discuss an algorithm for computing involutive HF-hat using bordered Floer homology and a proposed definition of bordered involutive Floer homology. This is joint work with Kristen Hendricks.
  
  On peculiar modules for 4-ended tangles, Claudius Zibrowius
  A peculiar module is a certain invariant of 4-ended tangles that I developed in my PhD thesis as a tool for studying the local behaviour of Heegaard Floer homology for knots and links. I will briefly explain its construction and then discuss two or three features of interest, such as mutation symmetries, skein relations and the role of the Fukaya category of the 4-punctured sphere.
  
  
• Wednesday June 14
  
  Universal Circles, Danny Calegari
  
  Braid groups and categorical actions, Tony Licata
  Braid groups (and, more generally, Artin groups of Coxeter groups) arise naturally in modern representation theory as "categorical reflection groups" acting on triangulated categories by "categorical reflections." The goal of this talk will be to explain how to see various structures of interest in the study of braid groups using their appearance as categorical reflection groups.
  
  Knot traces and concordance, Allison Miller
  A conjecture of Akbulut and Kirby from 1978 states that the concordance class of a knot is determined by its 0-surgery. In 2015, Yasui disproved this conjecture by providing pairs of knots which have the same 0-surgeries yet which can be distinguished in (smooth) concordance by an invariant associated to the four-dimensional traces of such a surgery. In this talk, I will discuss joint work with Lisa Piccirillo in which we construct many pairs of knots which have diffeomorphic 0-surgery traces yet some of which can be distinguished in smooth concordance by the Heegaard Floer d-invariants of their double branched covers. If time permits, I will also discuss the applicability of this work to the existence of interesting invertible satellite maps on the smooth concordance group.
  
  Pseudo-Anosov maps with small entropy and the curve complex, Vaibhav Gadre
  The talk will survey the theory of pseudo-Anosov maps with small entropy subsequently focussing on deriving bounds in terms of genus for small translation distances in the curve complex. The main result is joint work with Chia-yen Tsai
  
  Orderability questions in contact geometry, Vincent Colin
  I will review various results regarding orderability of the group of contactomorphisms of a contact manifolds and of the space of Legendrian submanifolds. This includes a work of Liu as well as joint work with Ferrand-Pushkar and Chantraine-Dimitroglou Rizell.
• Thursday June 15
  
  A topological invariant for left orders, Sarah Rasmussen
  I will discuss work in progress involving a topological invariant for left invariant orders on the fundamental group of a 3-manifold. This invariant measures an obstruction for producing a taut foliation from a left order.
  
  An Odd Khovanov Homotopy Type, Matt Stoffregen
  We define an odd Khovanov homotopy type, in analogy with the version of the (even) Khovanov homotopy type constructed by Lawson-Lipshitz-Sarkar, and list some of its basic properties, as well as conjectural relationships with other invariants. This is work in progress with Sucharit Sarkar and Chris Scaduto.
  
  Non L-spaces and spectral geometry, Francesco Lin
  We discuss an application of monopole Floer homology to the spectral geometry of three-manifolds: on a rational homology sphere which is not an L-space, for every Riemannian metric the first eigenvalue of the Laplacian on coexact one forms is bounded above very explicitly in terms of the Ricci curvature.
  
  
• Friday June 16
  
  Satellite L-space knots are braided satellites, Ken Baker
  Let {K_n} be the family of knots obtained by twisting a knot K along an unknot c. When the winding number of K about c is non-zero, we show the limit of g(K_n)/g₄(K_n) is 1 if and only if the winding and wrapping numbers of K about c are equal. When equal, this leads to a description of minimal genus Seifert surfaces of K_n for |n|>>0 and eventually to a characterization of when c is a braid axis for K. We then use this characterization to show that satellite L-space knots are braided satellites. This is joint work with Kimihiko Motegi that builds upon joint work with Scott Taylor.
  
  Knots with infinitely many SU(2)-cyclic surgeries, Steven Sivek
  The cyclic surgery theorem of Culler, Gordon, Luecke, and Shalen implies that any knot in S³ other than a torus knot has at most two nontrivial cyclic surgeries. In this talk, we investigate the weaker notion of SU(2)-cyclic surgeries on a knot, meaning surgeries whose fundamental groups only admit SU(2) representations with cyclic image. We will show that if a nontrivial knot in S³ has infinitely many SU(2)-cyclic surgeries, then the corresponding slopes (viewed as a subset of RP¹) have a unique limit point, which is a finite, rational number, and that this limit is a boundary slope for the knot. As a corollary, it follows that for any nontrivial knot, the set of SU(2)-cyclic surgery slopes is bounded. This is joint work with Raphael Zentner.
  
  Khovanov homology detects the trefoil, John Baldwin
  In 2010, Kronheimer and Mrowka proved that Khovanov homology detects the unknot, answering a "categorified" version of the famous open question: Does the Jones polynomial detect the unknot? An even more difficult question is: Does the Jones polynomial detects the trefoils? The goal of this talk is to outline our proof that Khovanov homology detects the trefoils, answering a "categorified" version of this second question. Our proof, like Kronheimer and Mrowka's, relies on a relationship between Khovanov homology and instanton Floer homology. More surprising, however, is that it also hinges fundamentally on several ideas from contact and symplectic geometry. This is joint work with Steven Sivek.
  
  Filtering the Heegaard Floer contact invariant, Gordana Matić
  We will explore a filtration on a stabilized Heegaard Floer complex associated with an open book decomposition compatible with a contact structure to define a new contact invariant "spectral order" which refines the Ozsvath-Szabo contact class. The definition is partially motivated by Hutcthings' interpretation of Algebraic Torsion of Latchev and Wendl. The spectral order is zero when the structure is over twisted, infinite when it is Stein fillable, and is often nonzero and gives us more information when the Ozsvath-Szabo contact invariant is zero but the contact structure is tight. This is joint work with Cagatay Kutluhan, Jeremy Van Horn-Morris and Andy Wand.
  
  Concordance of knots in homology spheres, Adam Levine
  Every knot in the 3-sphere bounds a non-locally flat piecewise-linear (PL) disk in the 4-ball, but Akbulut showed in 1990 that the same is not true for knots in the boundary of an arbitrary contractible 4-manifold. We strengthen this result by showing that there exists a knot K in a homology sphere Y (which is the boundary of a contractible 4-manifold) such that K does not bound a PL disk in any homology 4-ball bounded by Y. In more recent work (joint with Jen Hom and Tye Lidman), we show that the group of knots in homology spheres modulo non-locally-flat PL concordance contains an infinite cyclic subgroup.

Organisers

• Brendan Owens, Liam Watson.

Funding

• We gratefully acknowledge support from the European Commission (Marie Curie career integration grant HFFUNDGRP) and the School of Mathematics and Statistics at the University of Glasgow.