Touching Circles

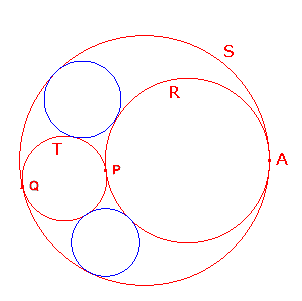
In the introductory page, we mentioned a problem about circles touching three mutually tangent circles. We are now in a position to give a proof. Theorem If three circles R, S and T touch at A, P and Q as shown, then there are exactly two circles which touch all of them. Of course, the proof consists of inversing in a circle to make the picture simpler.
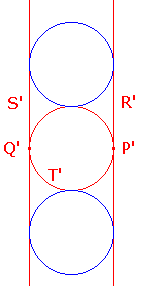
Proof Let C be a circle with centre A. Inverting in C sends A to Ñ, so R and S map to extended lines R' and S'. As A is not on T, T must map to a circle T' touching R' at P and S' at Q'. Any circle touching R' and S' must be have its center on the bisector of P'Q', and radius ½P'Q'. so there are exactly two touching T'. Inverting again in C, we get the circles touching R, S and T.

Main inversive page