Pascal's Theorem

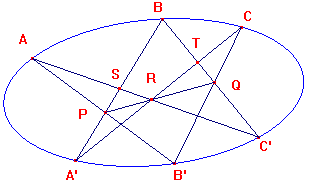
Pascal's Theorem
If A,A',B'B',C,C' lie on a conic C and AB',A'B meet in P,
BC',B'C in Q and CA',C'A in R, then P,Q,R are collinear.

proof
By Chasles' Theorem, (AA',AB',AC',AB) = (CA',CB',CC',CB).
As remarked above, these are equal to the cross-ratios of
the points which are intersections of the pencils with BA', BC'.
Thus (A',P,S,B) = (T,Q,C',B).
Now consider these cross-ratios as those of pencils through R.
(RA',RP,RA,RB) = (RC,RQ,RC',RB). As lines, RA'=RC, RA=RC',
so the pencils have three lines in common. Since their cross-
ratios are equal, the lines RP,RQ are identical, as required.